贝塔分布

本文解释了什么是 Beta 发行版以及它的用途。同样，您将能够看到 beta 分布图以及此类概率分布的属性。

什么是贝塔分布？

beta 分布是在区间 (0,1) 上定义的概率分布，并由两个正参数 α 和 β 参数化。换句话说，β分布的值取决于参数α和β。

因此，β分布的主要特点是其形状可以由参数α和β控制。此外，β 分布用于定义值在 0 到 1 之间的随机变量。

有几种表示法表明连续随机变量受 beta 分布支配，最常见的是：

在统计学中，β 分布的应用非常广泛。例如，β 分布用于研究不同样本中百分比的变化。同样，在项目管理中，β分布用于进行Pert分析。

贝塔分布图

考虑到 beta 分布的定义，beta 分布的密度函数和概率分布函数如下图所示。

下面您可以看到 beta 分布的密度函数图如何根据参数 α 和 β 变化。

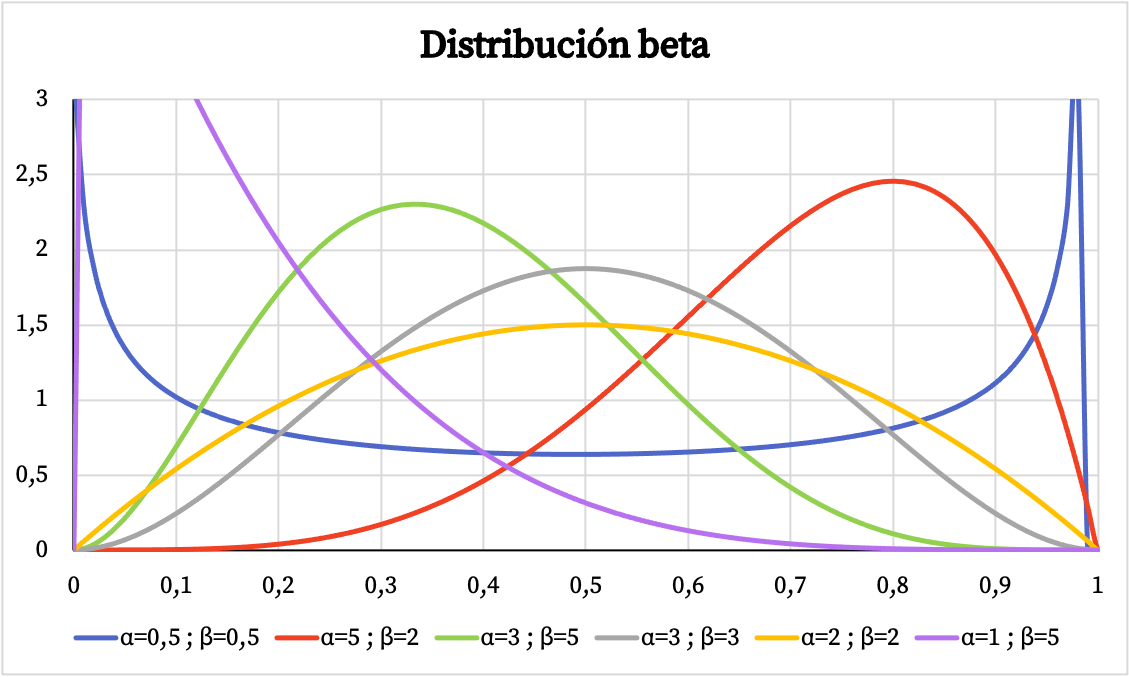
同样，下面您可以看到基于参数 α 和 β 的 beta 分布的累积概率的图形表示。

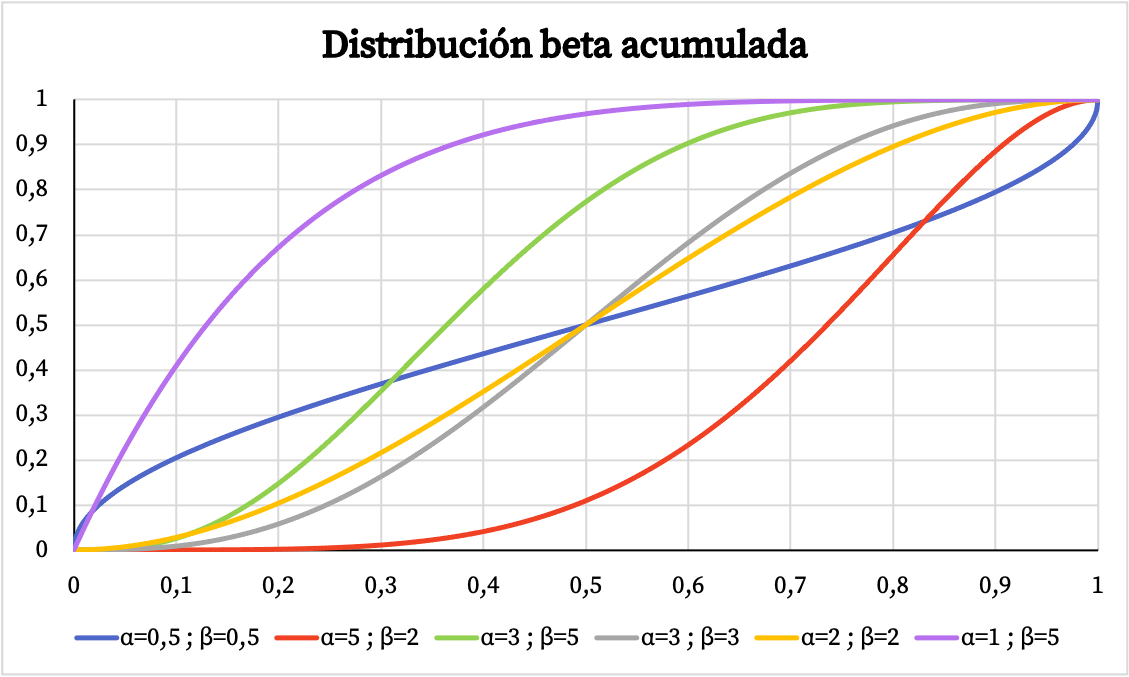
贝塔分布的特征

在本节中，我们将了解 beta 分布最重要的特征是什么。

• beta 分布的参数 α 和 β 是正实数。

• beta 分布的平均值等于 alpha 除以 alpha 加 beta 之和。

• beta 分布的方差可以使用以下公式计算：

• 对于大于 1 的 alpha 和 beta 值，可以通过以下表达式轻松找到 beta 分布模式：

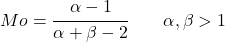
其中B(α,β)是β函数，定义为：

• Beta 分布的累积概率函数为：

其中B(x;α,β)是不完全beta函数，定义为：

• 如果 X 是由 beta 分布定义的变量，则 1-X 是由 beta 分布定义的变量，其 alpha 和 beta 参数分别是原始 beta 分布的 beta 和 alpha 参数。

• 如果 beta 分布的 alpha 和 beta 参数都等于 1，则该分布相当于参数 0 和 1 的均匀分布。