负二项分布
本文解释什么是负二项分布及其用途。您还将找到负二项式分布的公式、具体示例以及此类概率分布的属性。最后,您将能够使用在线计算器计算任何负二项分布概率。
什么是负二项分布?
负二项分布是一种概率分布,描述获得给定数量的正结果所需的伯努利试验次数。
因此,负二项式分布具有两个特征参数: r是期望的成功结果的数量, p是执行的每个伯努利实验的成功概率。
![]()
请记住,伯努利测试是一种有两种可能结果的实验:“成功”和“失败”。因此,如果“成功”的概率为p ,则“失败”的概率为q=1-p 。
因此,负二项分布定义了一个过程,其中根据需要进行尽可能多的伯努利试验以获得正结果。此外,所有这些伯努利试验都是独立的,并且成功的概率恒定。
例如,服从负二项式分布的随机变量是骰子必须滚动的次数,直到数字 6 滚动 3 次为止。
负二项分布与二项分布的区别在于,负二项分布统计的是获得一定数量成功结果所需的次数,而二项分布统计的是一系列伯努利测试中成功案例的数量。
➤请参阅:什么是二项分布?
负二项分布公式
给定参数r、p、x,负二项分布的概率通过将xr中的x-1的组合数乘以(1-p) xr再乘以p r来计算。
因此,计算负二项分布概率的公式为:

👉您可以使用下面的计算器来计算变量服从负二项式分布的概率。
负二项分布的求解练习
- 如果你抛一枚硬币八次,第八次抛硬币第四次出现正面的概率是多少?
首先,我们需要计算抛硬币时正面朝上的概率。在这种情况下,我们在两种可能的结果(正面和反面)中只有一个正面结果(正面),因此成功的概率为:
![]()
因此,该问题中的随机变量遵循负二项式分布,其中 r=4 且 p=0.5。因此,我们使用负二项分布公式来计算练习要求我们做的概率。
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-bc56100604e5889a6d169c0395f19ebe_l3.png)
负二项分布的特征
以下是负二项分布的最重要特征。
- 负二项式分布由两个特征参数定义: r是期望的成功结果的数量, p是执行的每个伯努利实验的成功概率。
*** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.
- 负二项分布的方差等于r乘以(1-p)除以p 2 。
![]()
- 如果参数r大于1,则负二项分布的众数可以通过以下公式计算:
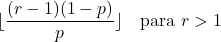
![]()
- 负二项分布的偏度系数由以下表达式计算:
![]()
- 负二项分布的峰度可以通过以下公式计算:
![]()
- 如果参数r等于 1,则我们有几何分布的情况。
![]()
负二项分布计算器
将参数r、p、x的值输入到下面的计算器中,计算概率。您必须使用点作为小数分隔符输入数字,例如 0.50。