逻辑回归简介
当我们想要了解一个或多个预测变量与连续响应变量之间的关系时,我们经常使用线性回归。
但是,当响应变量是分类变量时,我们可以使用逻辑回归。
逻辑回归是一种分类算法,因为它尝试将数据集中的观察结果“分类”为不同的类别。
以下是使用逻辑回归的一些示例:
- 我们希望使用信用评分和银行余额来预测特定客户是否会拖欠贷款。 (响应变量=“默认”或“无默认”)
- 我们希望使用场均篮板数和场均得分来预测特定篮球运动员是否会被选入 NBA(响应变量 =“选秀”或“未选秀”)。
- 我们想要使用平方英尺和浴室数量来预测某个城市的房屋是否会以 200,000 美元或更高的售价列出。 (响应变量=“是”或“否”)
请注意,每个示例中的响应变量只能采用两个值之一。将此与响应变量取连续值的线性回归进行比较。
逻辑回归方程
逻辑回归使用一种称为最大似然估计的方法(这里不讨论细节)来找到以下形式的方程:
log[p(X) / ( 1 -p(X))] = β 0 + β 1 X 1 + β 2 X 2 + … + β p
金子:
- X j :第 j个预测变量
- β j :第 j个预测变量的系数估计
方程右侧的公式预测响应变量取值 1 的对数几率。
因此,当我们拟合逻辑回归模型时,我们可以使用以下方程来计算给定观测值为 1 的概率:
p(X) = e β 0 + β 1 X 1 + β 2 X 2 + … + β p
然后我们使用一定的概率阈值将观察结果分类为 1 或 0。
例如,我们可以说概率大于或等于 0.5 的观测值将被分类为“1”,所有其他观测值将被分类为“0”。
如何解释逻辑回归的结果
假设我们使用逻辑回归模型根据给定篮球运动员的场均篮板数和场均得分来预测他是否会被选入 NBA。
这是逻辑回归模型的结果:
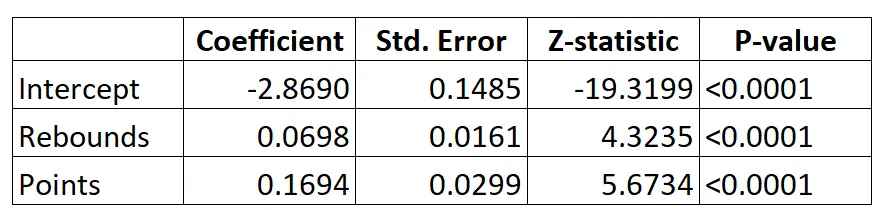
使用这些系数,我们可以使用以下公式根据特定球员的平均篮板数和场均得分来计算其被选入 NBA 的概率:
P(选秀) = e -2.8690 + 0.0698*(篮板) + 0.1694*(分) / (1+e -2.8690 + 0.0698*(篮板) + 0.1694*(分) ) )
例如,假设某位球员场均 8 个篮板和 15 分。根据模型,该球员被选入 NBA 的概率为0.557 。
P(书面) = e -2.8690 + 0.0698*(8) + 0.1694*(15) / (1+e -2.8690 + 0.0698*(8) + 0.1694*(15 ) ) = 0.557
由于该概率大于 0.5,因此我们预测该球员将被选中。
相比之下,一名场均仅得到 3 个篮板和 7 分的球员。该球员被选入 NBA 的概率为0.186 。
P(书面) = e -2.8690 + 0.0698*(3) + 0.1694*(7) / (1+e -2.8690 + 0.0698*(3) + 0.1694*(7 ) ) = 0.186
由于这个概率小于 0.5,我们预测该球员不会被选中。
逻辑回归假设
逻辑回归使用以下假设:
1. 响应变量是二进制的。假设响应变量只能采取两种可能的结果。
2. 观察是独立的。假设数据集中的观测值彼此独立。也就是说,观察结果不应来自对同一个人的重复测量,也不应以任何方式相互关联。
3.预测变量之间不存在严重的多重共线性。假设没有一个预测变量彼此高度相关。
4.不存在极端异常值。假设数据集中不存在极端异常值或有影响的观测值。
5. 预测变量和响应变量的 logit 之间存在线性关系。可以使用 Box-Tidwell 检验来检验该假设。
6.样本量足够大。通常,每个解释变量应该至少有 10 个具有最不常见结果的案例。例如,如果您有 3 个解释变量,并且最不常见结果的预期概率为 0.20,则您的样本量应至少为 (10*3) / 0.20 = 150。
查看 这篇文章,了解如何验证这些假设的详细说明。