逻辑回归与线性回归：主要区别

最常用的两种回归模型是线性回归和逻辑回归。

两种类型的回归模型都用于量化一个或多个预测变量与响应变量之间的关系，但这两种模型之间存在一些关键区别：

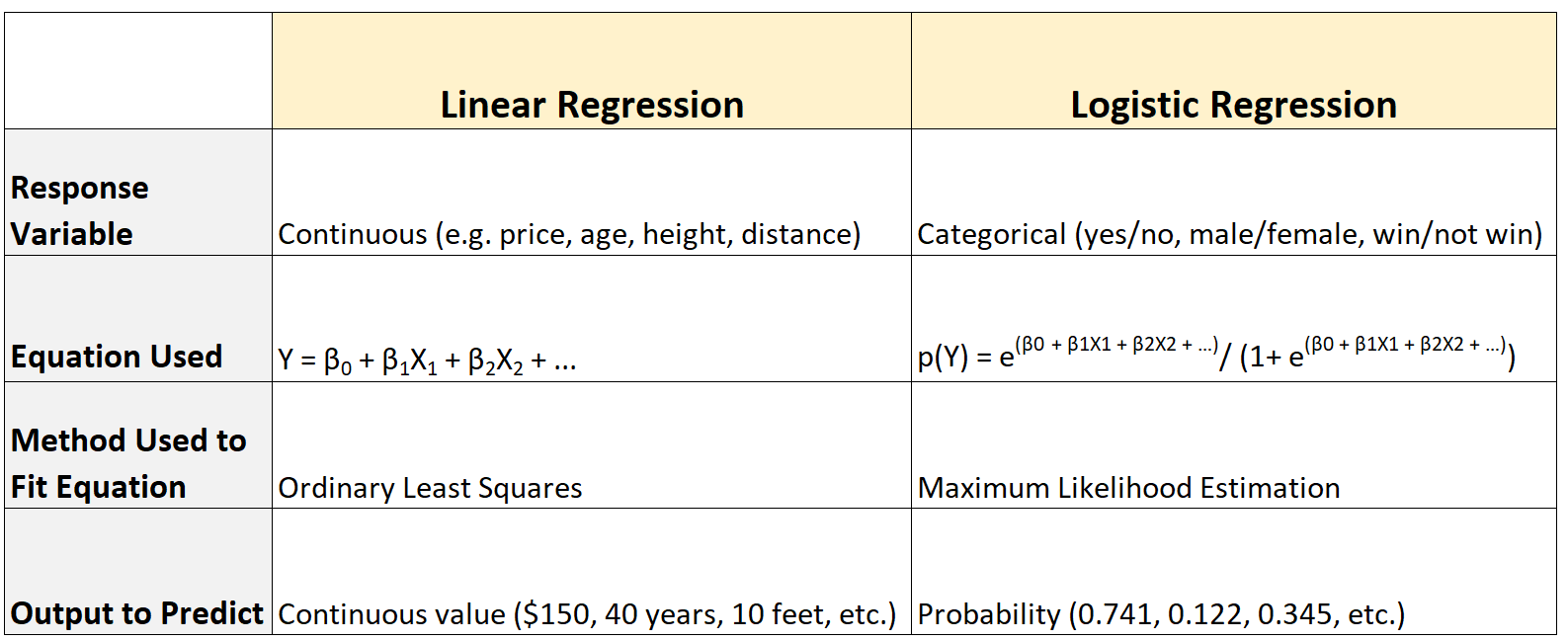
以下是差异摘要：

差异#1：响应变量类型

当响应变量采用连续值时，使用线性回归模型：

• 价格
• 高度
• 年龄
• 距离

相反，当响应变量采用分类值时，使用逻辑回归模型，例如：

• 是还是不是
• 男女不限
• 赢还是不赢

差异#2：使用的方程

线性回归使用以下方程来总结预测变量和响应变量之间的关系：

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

金子：

• Y：响应变量
• X _j ：第 j^个预测变量
• β _j ：在保持所有其他预测变量不变的情况下，X _j增加 1 个单位对 Y 的平均影响

相反，逻辑回归使用以下方程：

p(X) = e ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

该方程用于预测单个观察结果属于某个类别的概率。

差异#3：用于拟合方程的方法

线性回归使用称为普通最小二乘法的方法来查找最佳拟合回归方程。

相反，逻辑回归使用一种称为最大似然估计的方法来查找最佳拟合回归方程。

差异#4：要预测的输出

线性回归预测连续值作为输出。例如：

• 价格（150 美元、199 美元、400 美元等）
• 高度（14 英寸、2 英尺、94.32 厘米等）
• 年龄（2个月、6岁、41.5岁等）
• 距离（1.23 英里、4.5 公里等）

相反，逻辑回归预测概率作为结果。例如：

• 被大学录取的几率为 40.3%。
• 赢得一场比赛的几率为 93.2%。
• 法律通过的可能性为 34.2%。

何时使用逻辑回归或线性回归

以下练习题可以帮助您更好地理解何时使用逻辑回归或线性回归。

问题#1：年收入

假设一位经济学家想要使用预测变量 (1) 每周工作时间和 (2) 受教育年限来预测个人的年收入。

在这种情况下，他将使用线性回归，因为响应变量（年收入）是连续的。

问题#2：大学录取

假设一名大学招生官员想要使用预测变量 (1) GPA 和 (2) ACT 分数来预测学生被某所大学录取的可能性。

在这种情况下，她将使用逻辑回归，因为响应变量是分类变量，只能采用两个值：接受或不接受。

问题#3：房地产价格

假设房地产经纪人想要使用预测变量 (1) 平方英尺、(2) 卧室数量和 (3) 浴室数量来预测房屋销售价格。

在这种情况下，她将使用线性回归，因为响应变量（价格）是连续的。

问题#4：垃圾邮件检测

假设计算机程序员想要使用预测变量 (1) 字数和 (2) 来源国家/地区来预测给定电子邮件是垃圾邮件的概率。

在这种情况下，它将使用逻辑回归，因为响应变量是分类变量，并且只能采用两个值：垃圾邮件或非垃圾邮件。

其他资源

以下教程提供了有关线性回归的更多详细信息：

• 简单线性回归简介
• 多元线性回归简介
• 现实生活中使用线性回归的 4 个示例

以下教程提供了有关逻辑回归的更多详细信息：

• 逻辑回归简介
• 现实生活中使用逻辑回归的 4 个示例