重复测量方差分析的三个假设
重复测量方差分析用于确定三个或更多组的平均值之间是否存在统计显着性差异，其中每组中出现相同的受试者。
然而，在执行重复测量方差分析之前，我们必须确保满足以下假设：
1. 独立性：每个观察必须是独立的。
2.正态性：响应变量的分布呈正态分布。
3. 球形度：相关组的所有组合之间的差异的方差必须相等。
如果违反这些假设中的一个或多个，则重复测量方差分析的结果可能不可靠。
在本文中，我们对每个假设进行了解释，如何确定假设是否满足，以及如果不满足该怎么办。
假设1：独立性
重复方差分析假设数据集中的每个观测值独立于所有其他观测值。
如何确定这个假设是否满足
验证这一假设的最简单方法是验证数据集中的每个个体都是使用随机抽样方法从总体中随机抽样的。
如果使用随机抽样方法，则可以假设每次观察都是独立的。
如果不遵守此假设该怎么办
如果不满足这一假设，那么这是一个严重的问题，因为每个人的价值观可能以某种方式相互关联。
通常，这种情况下唯一的补救措施是使用随机抽样方法招募个人进行新研究。
假设2：正态性
如何确定这个假设是否满足
有两种方法可以检验这个假设是否正确：
1. 创建直方图或 QQ 图
您可以通过创建直方图或 QQ 图直观地检查响应变量的分布是否近似正态分布。
如果您创建直方图，只需检查响应变量的分布是否大致遵循“钟形”形状。如果是这样，您通常可以假设满足正态性假设：
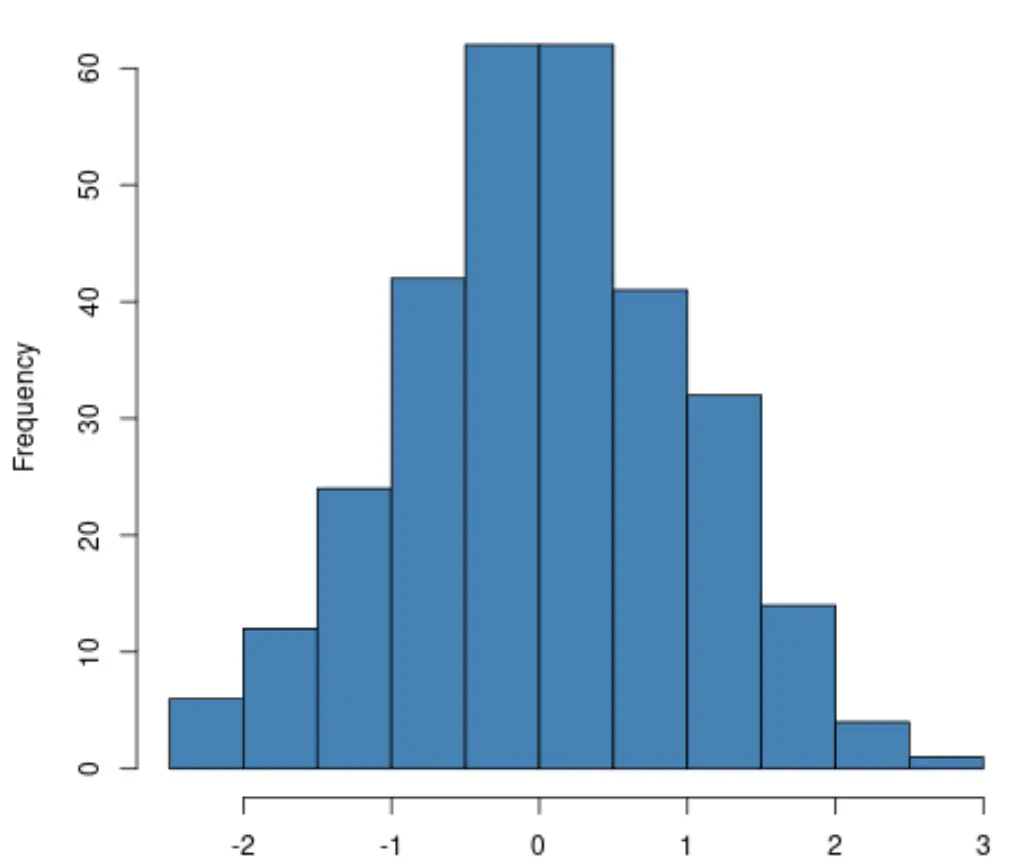
如果您要创建QQ 图，请检查数据点是否沿直线对角线分布。如果是这样，您通常可以假设满足正态性假设：
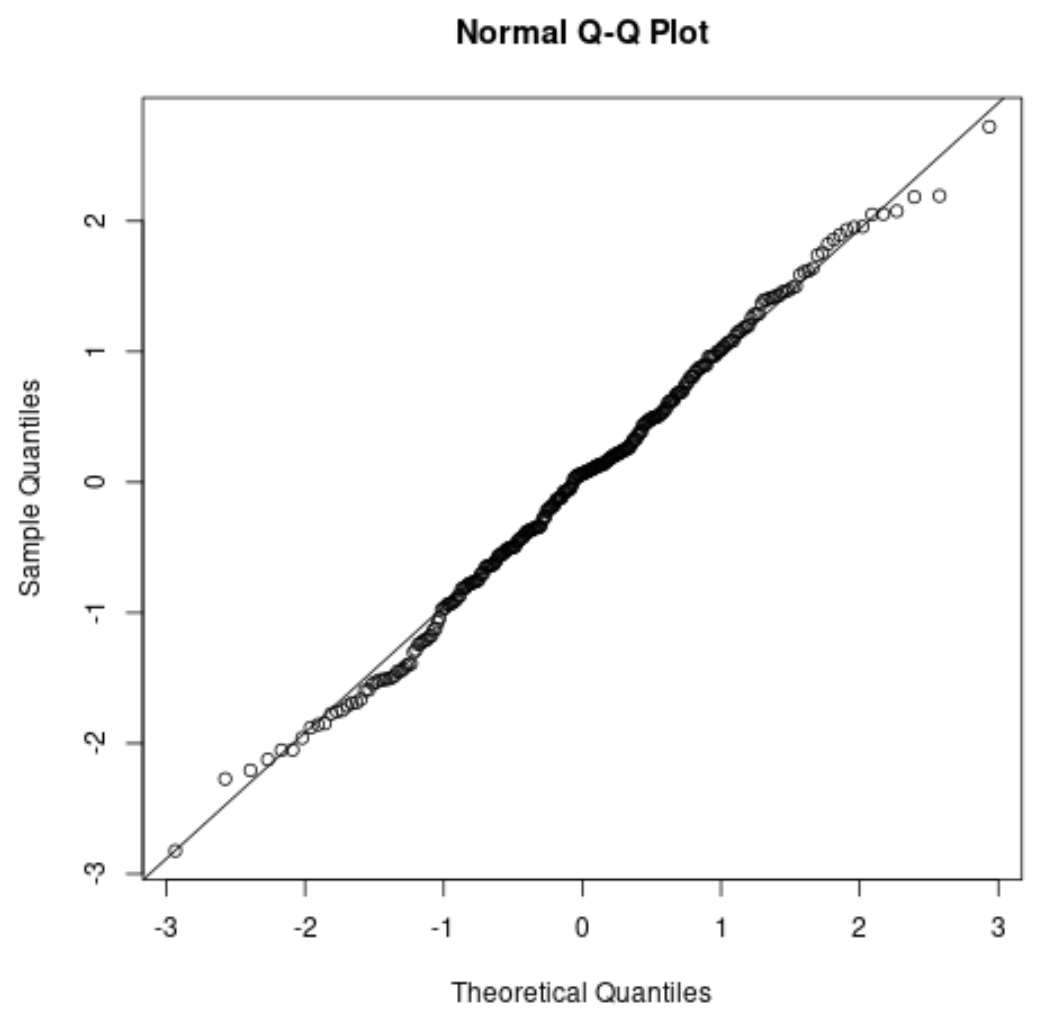
2. 进行正式的统计测试
您还可以执行Shapiro-Wilk 检验来检查正态性。如果检验的p 值小于 0.05，则表明数据不呈正态分布。
但是，请注意，在处理极大的样本时，夏皮罗-威尔克检验等统计检验几乎总是会告诉您数据不正常。
因此，通常最好使用直方图和 QQ 图等图表来直观地检查数据。只需查看图表，您就可以很好地了解数据是否服从正态分布。
如果不遵守此假设该怎么办
一般来说，只要样本量足够大，重复测量方差分析就被认为对于违反正态性假设非常稳健。
如果严重违反正态性假设，您有两种选择：
1.转换数据的响应值，使分布更加服从正态分布。
2.执行等效的非参数检验，例如不需要正态性假设的弗里德曼检验。
假设3：球形度
重复测量方差分析假设球形度，即相关组的所有组合之间的差异方差必须相等。
如果不满足这一假设，F 比就会夸大，重复测量方差分析的结果就会变得不可靠。
如何确定这个假设是否满足
为了检验这个假设是否成立，我们可以进行莫奇利球形度检验。
该检验使用以下原假设和备择假设：
- H 0 : 差异的方差相等
- H A : 差异的方差不相等
如果检验的 p 值低于一定的显着性水平（例如 α = 0.05），则我们拒绝原假设并得出差异方差不相等的结论。
否则，如果 p 值不小于一定的显着性水平（例如 α = 0.05），我们无法拒绝原假设并得出满足球形假设的结论。
根据您使用的统计软件，此测试的结果将如下所示：
由于 p 值不小于 0.05，我们将无法拒绝原假设并得出结论：在此特定示例中满足球形假设。
如果不遵守此假设该怎么办
如果我们拒绝莫奇利球形检验的零假设，我们通常会对用于计算重复测量方差分析表中 F 值的自由度进行修正。
我们可以应用三个修复：
- Huynh-Feldt（最不保守）
- 塞尔-盖塞尔
- 下限（最保守）
这些修正中的每一个都会增加重复测量方差分析输出表中的 p 值，以解释违反球形假设的事实。
然后我们可以使用这些 p 值来确定是否应该拒绝重复测量方差分析的原假设。
其他资源
以下教程提供有关重复测量方差分析的更多信息：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多