统计中的阻塞:定义和示例
通常在实验中,研究人员希望了解解释变量和响应变量之间的关系。
不幸的是,实验研究中经常出现干扰变量,这些变量影响解释变量和响应变量之间的关系,但研究人员并不感兴趣。
例如,假设研究人员想要了解新饮食对减肥的影响。解释变量是新的饮食习惯,响应变量是体重减轻的程度。
然而,一种可能导致变异的无序变量是性别。无论新饮食是否有效,个人的性别很可能会影响他们减掉的体重。
阻止概述
控制干扰变量影响的一种常见方法是通过分块,即根据干扰变量的值划分实验中的个体。
在前面的示例中,我们将个人放置在以下两个块之一中:
- 男性
- 女性
然后,在每个块内,我们将随机分配个体接受以下两种治疗之一:
- 新的饮食习惯
- 标准饮食
通过这样做,每个区块内的差异将远低于所有个体之间的差异,我们将能够更好地了解新饮食如何在控制性别的同时影响减肥。
为了说明这一点,请考虑下表,该表显示了参与该研究的 16 人的总体重减轻情况:
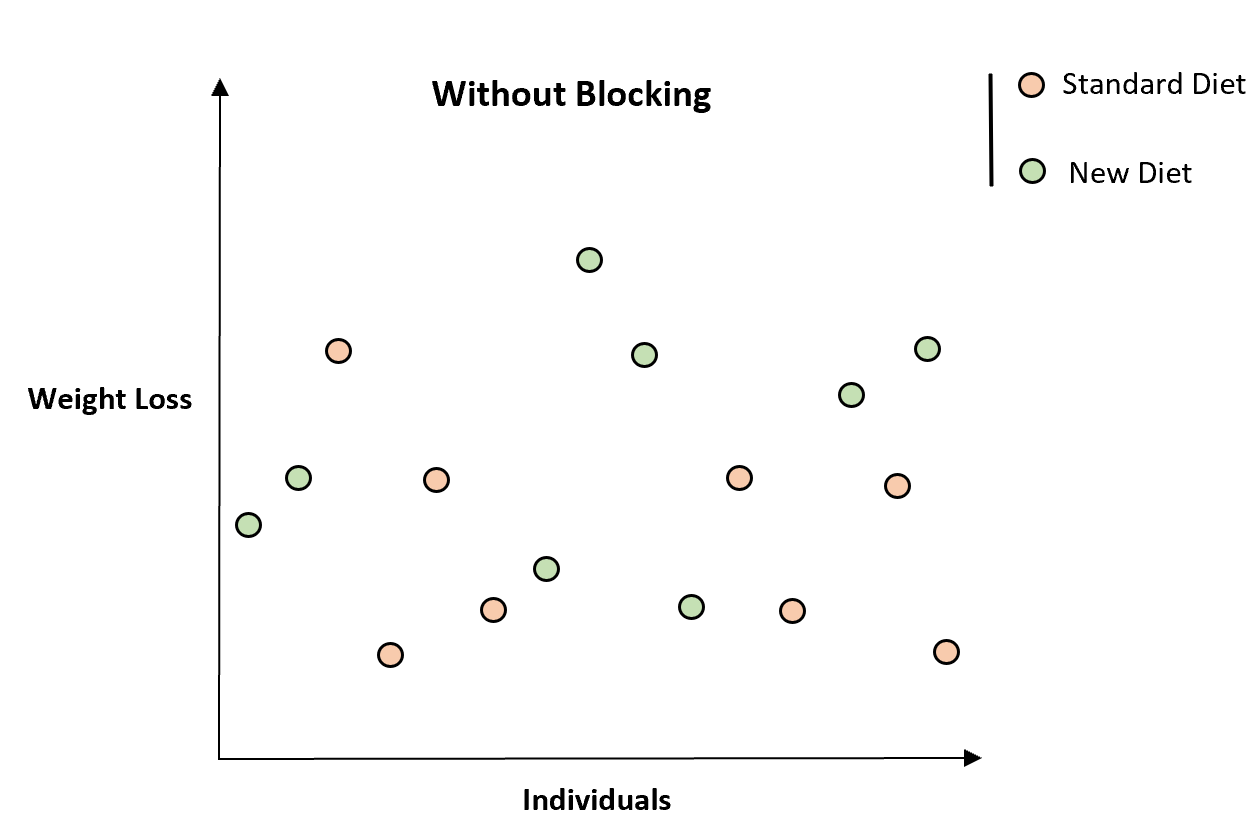
乍一看,新饮食似乎与体重减轻无关。
然而,一旦我们根据性别将个体分为两部分,很明显新的饮食似乎与体重减轻有关:
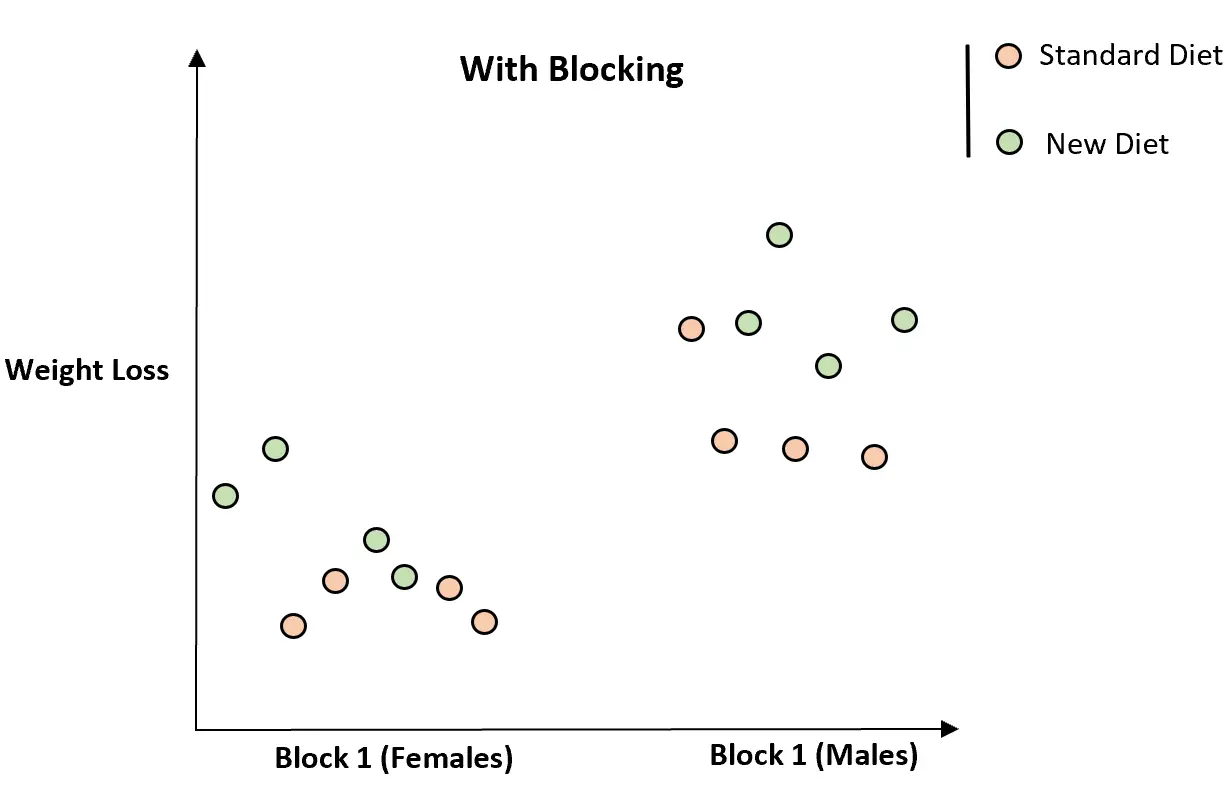
通过将个体分组,新饮食和减肥之间的关系变得更加清晰,因为我们能够控制性别的无序变量。
更多阻塞示例
性别是实验中常用的阻碍因素,因为男性和女性对各种治疗的反应往往不同。
然而,其他可用作阻塞因素的常见干扰变量包括:
- 年龄范围
- 收入组
- 教育程度
- 运动量
- 地区
根据实验的性质,也可以同时使用多个阻断因子。然而,实际上,通常只使用一两个,因为更多的阻塞因素需要更大的样本量才能获得有意义的结果。
有害变量和隐藏变量
在前面的例子中,性别是一个已知的紊乱变量,研究人员认为它会影响体重减轻。然而,在实验中通常还存在隐藏变量,这些变量也影响解释变量和响应变量之间的关系,但这些变量要么是未知的,要么根本不包括在研究中,因为很难收集它们的数据。
例如,我们假设每个人都有一些与生俱来的纪律,他们可以依靠这些纪律来减轻更多体重。由于纪律很难衡量,因此它没有作为研究中的阻碍因素包括在内,但控制它的一种方法是使用随机化。
通过将个体随机分配到新饮食或标准饮食中,研究人员可以最大限度地提高两组个体的整体纪律水平大致相等的机会。
因此,在任何使用分组的实验中,随机分配个体进行治疗以控制任何潜在隐藏变量的影响也很重要。