什么是随机变量？

随机变量，通常表示为X，是一个其可能值是随机过程结果的变量。

有两种类型的随机变量：离散变量和连续变量。

离散随机变量

离散随机变量是一种只能取可数个不同值的变量，例如 0、1、2、3、4、5…100、100 万等。以下是离散随机变量的一些示例：

• 一枚硬币抛掷 20 次后反面落地的次数。
• 骰子滚动 100 次后落在数字4上的次数。
• 一盒 50 个小部件中缺陷小部件的数量。

离散随机变量的概率分布告诉我们随机变量取特定值的概率。

例如，假设我们掷了一次公平骰子。如果我们让X表示骰子落在某个数字上的概率，那么概率分布可以写成如下：

• P(X=1)： 1/6
• P(X=2)： 1/6
• P(X=3)： 1/6
• P(X=4)： 1/6
• P(X=5)： 1/6
• P(X=6)： 1/6

笔记：

为了使概率分布有效，它必须满足以下两个标准：

1.每个结果的概率必须在 0 到 1 之间。

2.所有概率的总和必须为 1。

请注意，掷骰子的概率分布满足这两个标准：

1.每个结果的概率都在 0 到 1 之间。

2.所有概率的总和为 1。

我们可以使用直方图来可视化概率分布：

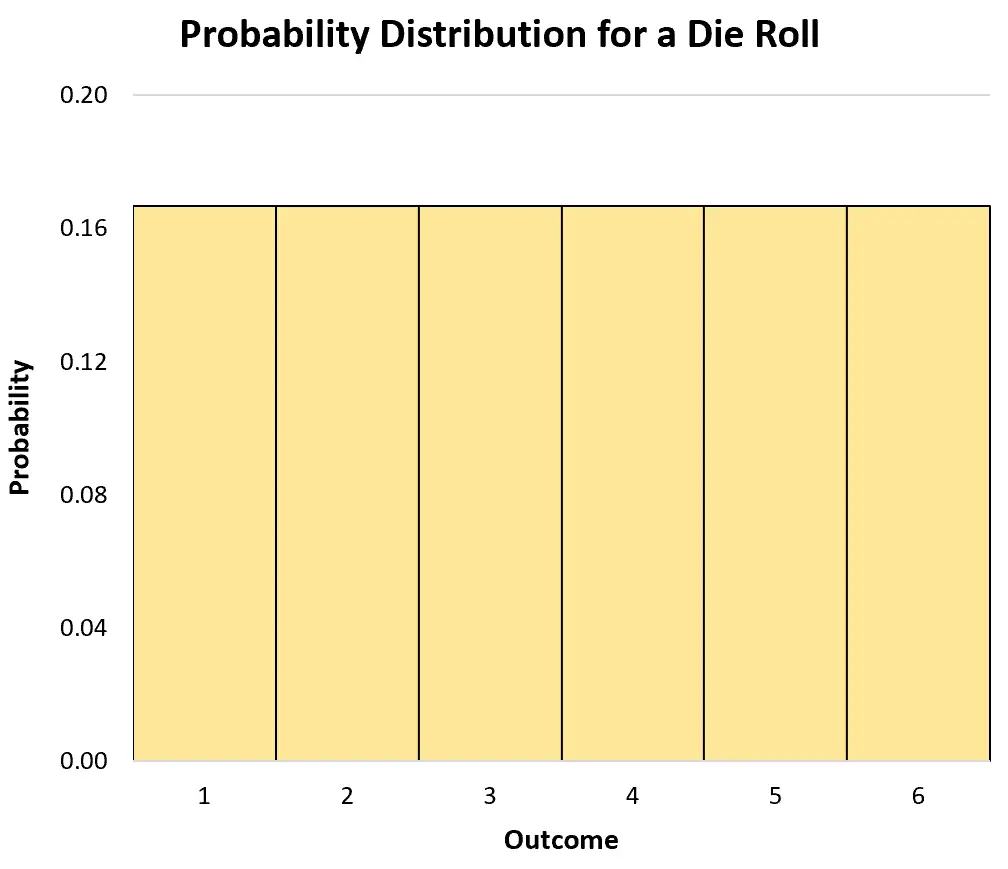
离散随机变量的累积概率分布告诉我们该变量的值等于或小于某个值的概率。

例如，掷骰子的累积概率分布如下所示：

• P(X≤1)： 1/6
• P(X≤2)： 2/6
• P(X≤3)： 3/6
• P(X≤4)： 4/6
• P(X≤5)： 5/6
• P(X≤6)： 6/6

骰子落在 1 或更少的数字上的几率仅为 1/6，因为它不能落在小于 1 的数字上。

落在两个或更少的物体上的概率为 P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6。

同样，它落在三个或更少的概率为 P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6，并且很快。

我们还可以使用直方图来可视化累积概率分布：

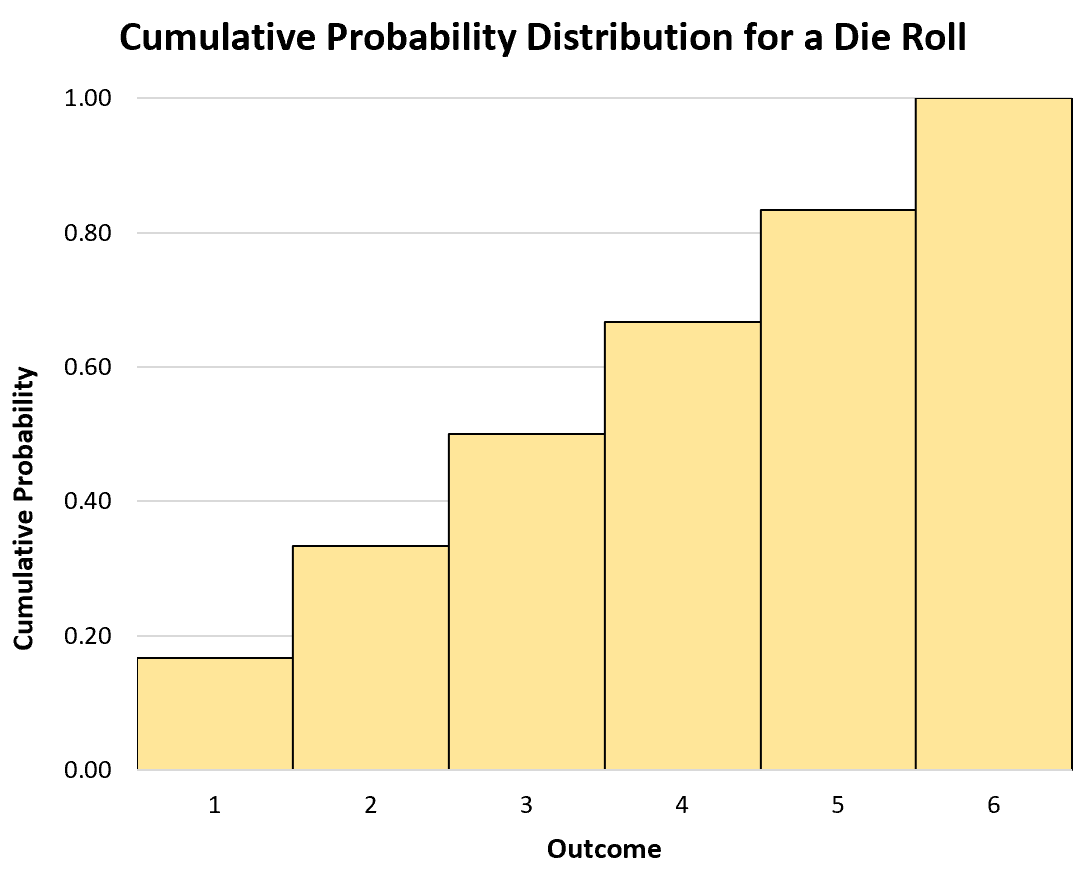
连续随机变量

连续随机变量是可以取无限多个可能值的变量。以下是连续随机变量的一些示例：

• 动物的体重
• 一个人的身高
• 跑马拉松所需时间

例如，一个人的身高可能是 60.2 英寸、65.2344 英寸、70.431222 英寸等。大小有无数可能的值。

一般规则：

如果您可以计算结果的数量，那么您正在使用离散随机变量 – 例如，计算硬币正面朝上的次数。

但如果您可以测量结果，那么您正在使用连续随机变量 – 例如测量身高、体重、时间等。

连续随机变量的概率分布告诉我们随机变量取特定值的概率。

然而，与离散随机变量的概率分布不同，连续随机变量的概率分布只能用于告诉我们该变量取一定范围值的概率。

例如，假设我们想知道特定餐厅的汉堡重四分之一磅（0.25 磅）的概率。由于重量是连续变量，因此它可以取无限多个值。

例如，给定的汉堡包实际上可能重 0.250001 磅、0.24 磅或 0.2488 磅。给定汉堡的重量恰好为 0.25 磅的概率基本上为零。

所以我们只能用概率分布来告诉我们一个汉堡重量小于0.25磅、大于0.25磅、或者在某个范围之间（例如在0.23磅到0.27磅之间）的概率。

其他资源

以下教程提供有关随机变量的其他信息：

什么是独立同分布随机变量？
现实生活中随机变量的 10 个例子