如何在 stata 中进行 mcnemar 检验
麦克尼马尔检验是我们可以用来确定配对数据之间的比例是否存在统计显着差异的检验。
本教程介绍如何在 Stata 中执行 McNemar 检验。
示例:Stata 中的 McNemar 检验
假设研究人员想知道某个营销视频是否可以改变人们对特定法律的看法。他们对 100 人进行了调查,看看他们是否支持这项法律。然后他们向所有 100 人播放营销视频,并在视频结束后再次对他们进行调查。
下表显示了观看视频前后支持该法律的总人数:
| 营销前的视频 | ||
|---|---|---|
| 营销后视频 | 支持 | 受不了 |
| 支持 | 30 | 40 |
| 受不了 | 12 | 18 |
为了确定观看视频前后支持法律的人数比例是否存在统计上的显着差异,我们可以进行麦克尼马尔检验。
在Stata中,我们可以使用mcci命令来进行McNemar检验。我们从左到右、从上到下将计数输入到 2×2 表中:
麦奇 30 40 12 18
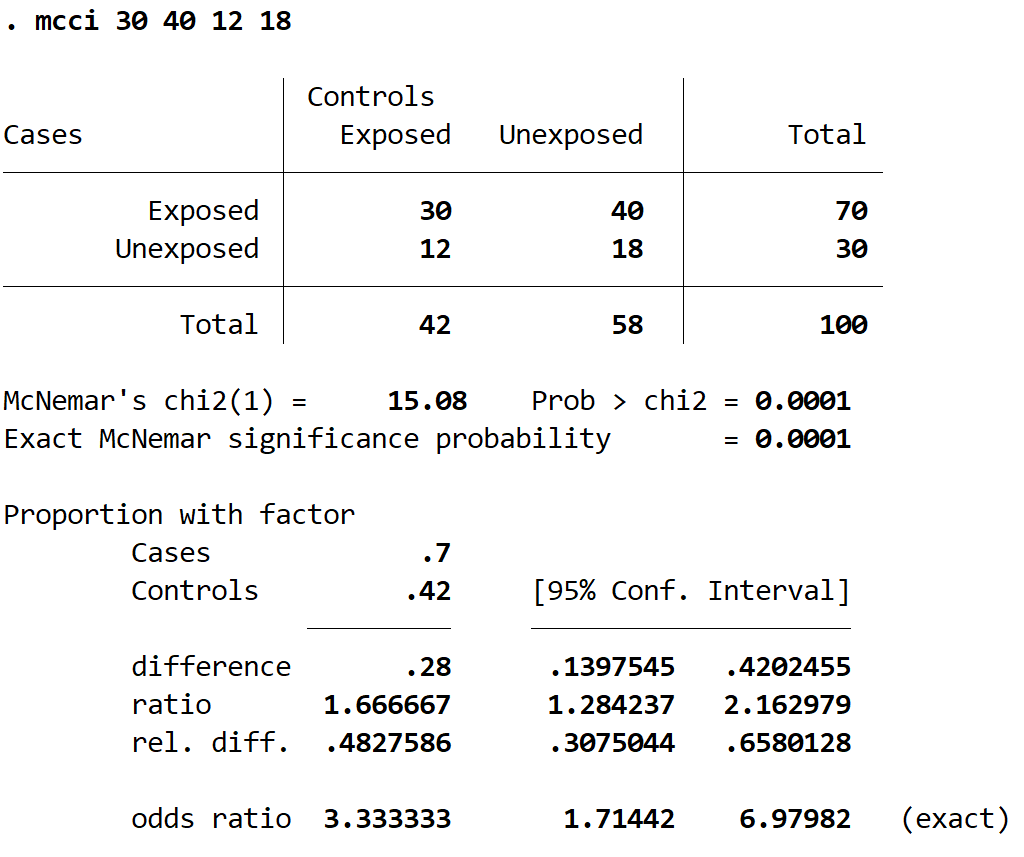
以下是如何解释结果:
2 × 2 表: Stata 使用病例对照研究中常见的传统标签显示 2 × 2 计数表。我们可以看到账户总数加起来是100。
McNemar 的 Chi2(1):这是卡方检验统计量,结果为 15.08。 Stata 使用以下公式计算该值:(40-12) 2 / (40+12) = 784 / 52 = 15.0769。
Prob > chi2:这是与卡方检验统计量相关的 p 值。结果是 0.0001。由于该值小于 0.05,因此我们可以拒绝原假设,并得出结论:在观看营销视频之前和之后支持该法律的人数比例在统计上存在显着差异。
关于计算卡方的注意事项
给定以下 2×2 表:
| 营销前的视频 | ||
|---|---|---|
| 营销后视频 | 支持 | 受不了 |
| 支持 | 有 | 乙 |
| 受不了 | VS | D |
Stata 使用公式 (BC) 2 / (B+C) 来计算卡方检验统计量。
然而,一些统计教科书建议当表中的某些数字较小时,使用公式 (|BC| – 1) 2 / (B+C) 作为连续性校正。通常,当单元格数量小于 5 时,通常会应用此校正。