完整指南：2×4 因子设计

2 × 4 因子设计是一种实验设计，可让研究人员了解两个自变量对单个因变量的影响。

在这种类型的设计中，一个自变量有两个水平，另一个自变量有四个水平。

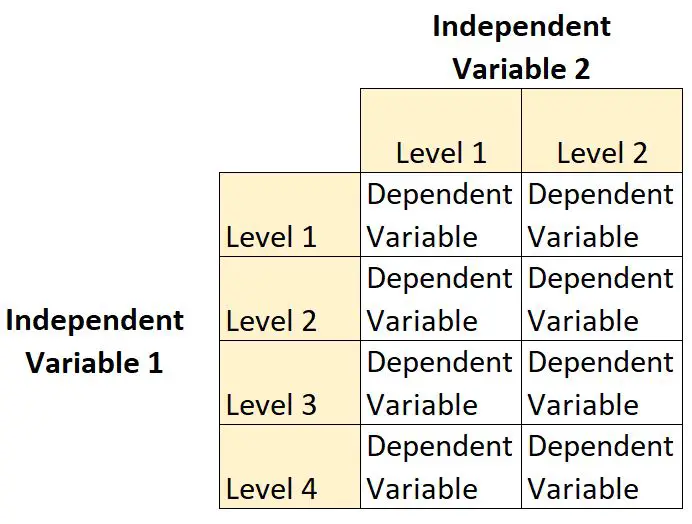
例如，假设植物学家想要了解阳光（无阳光、低阳光、中阳光或高阳光）和浇水频率（每天或每周）对某种植物物种生长的影响。

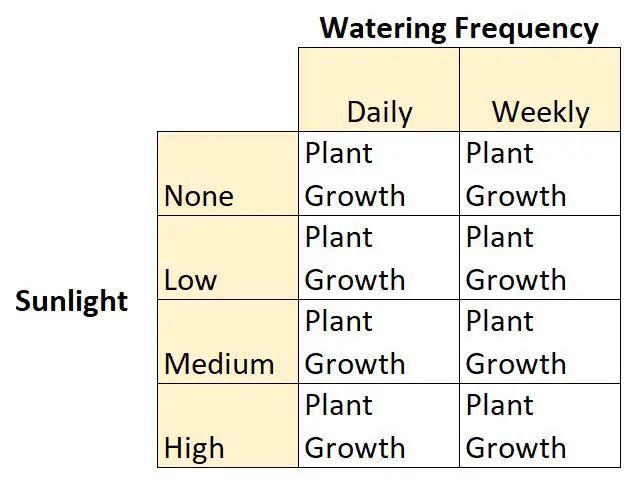
这是 2 × 4 因子设计的示例，因为有两个自变量，一个有两个水平，一个有四个水平：

• 自变量#1：阳光
  • 级别：无、低、中、高
• 自变量#2：浇水频率
  • 级别：每日、每周

还有一个因变量：植物生长。

2 × 4 因子设计的目的

2×4 因子设计可以分析以下效应：

主效应：这些是单个自变量对因变量的影响。

例如，在我们之前的场景中，我们可以分析以下主要影响：

• 阳光对植物生长的主要影响。
  • 所有没有接受阳光的植物的平均生长情况。
  • 所有接受低光照的植物的平均生长情况。
  • 所有接受平均阳光照射的植物的平均生长情况。
  • 所有接受强阳光照射的植物的平均生长情况。
• 浇水频率对植物生长的主要影响。
  • 每天浇水的所有植物的平均生长情况。
  • 每周浇水的所有植物的平均生长情况。

交互效应：当一个自变量对因变量的影响取决于另一个自变量的水平时，就会发生交互效应。

例如，在我们之前的场景中，我们可以分析以下交互效果：

• 阳光对植物生长的影响取决于浇水频率吗？
• 浇水频率对植物生长的影响取决于阳光吗？

如何分析 2 × 4 因子设计

我们可以执行双向方差分析来正式测试自变量与因变量是否具有统计显着关系。

例如，以下代码显示了如何在 R 中对假设的工厂场景执行双向方差分析：

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' None ', ' Low ', ' Medium ', ' High '), each= 10 , times= 2 ),
                 water = rep(c(' Daily ', ' Weekly '), each= 40 , times= 2 ),
                 growth = c(rnorm(10, 8, 2), rnorm(10, 8, 3), rnorm(10, 13, 2),
                            rnorm(10, 14, 3), rnorm(10, 10, 4), rnorm(10, 12, 3),
                            rnorm(10, 13, 2), rnorm(10, 14, 4)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 3 744.1 248.04 34.16 < 2e-16 ***
water 1 43.1 43.05 5.93 0.016 *  
sunlight:water 3 195.8 65.27 8.99 1.61e-05 ***
Residuals 152 1103.5 7.26                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

以下是解释方差分析结果的方法：

主要效应#1（阳光） ：与阳光相关的 p 值为<2e-16 。由于这个数字小于0.05，这意味着暴露在阳光下对植物生长具有统计上显着的影响。

主效应#2（水） ：与水相关的 p 值为0.016 。由于这个数字小于0.05，这意味着浇水频率对植物生长也有统计上显着的影响。

相互作用效应：阳光和水之间相互作用的 p 值为0.000061 。由于该值小于0.05，说明阳光与水之间存在相互作用效应。

其他资源

以下教程提供有关实验设计和分析的更多信息：

完整指南：2 × 2 因子设计
完整指南：2 × 3 因子设计
什么是阶乘方差分析？