散点图

本文解释什么是散点图。因此，您将了解点云的用途、如何创建点云、如何解释它以及点云的示例。

什么是点云？

散点图或散点图是一种统计图，其中两个变量的数据集在两个笛卡尔坐标轴上绘制。

因此，散点图用于分析两个统计变量之间的关系。

散点图有几个不同的名称，例如相关图或散点图。

需要注意的是，散点图被认为是质量控制的基本工具之一，就像帕累托图、因果图、流程图等一样。

如何制作散点图

要创建散点图，您需要执行以下步骤：

1. 从您想要分析的样本中收集统计数据。请记住，要创建散点图，必须至少有两个定量变量。
2. 绘制散点图的两个轴。
3. 确定将绘制图表的两个统计变量。
4. 校准图表每个轴的比例。为此，建议首先找到每个变量的最小值和最大值，然后根据这些值缩放每个轴。
5. 用一个点表示散点图上的每对数据。
6. 分析并解释获得的散点图。

散点图示例

在了解散点图的定义及其创建理论之后，本节将展示这种类型的图表作为示例。

• 在下面的频数表中，收集了 20 名学生的数学和统计成绩作为数据。将数据集绘制在散点图上并进行分析。

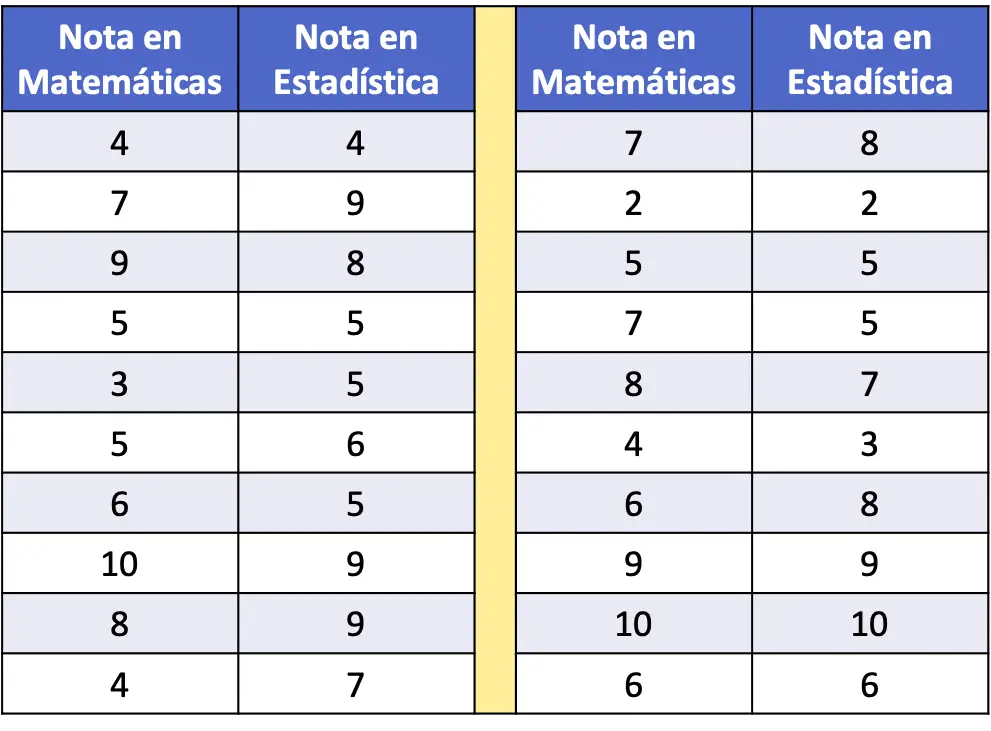
要在散点图中表示数据系列，我们只需绘制两个轴，校准它们，然后在图表上为每对数据绘制一个点。请记住，图表上的一个点位于与其每个值对应的假想线的交点处。

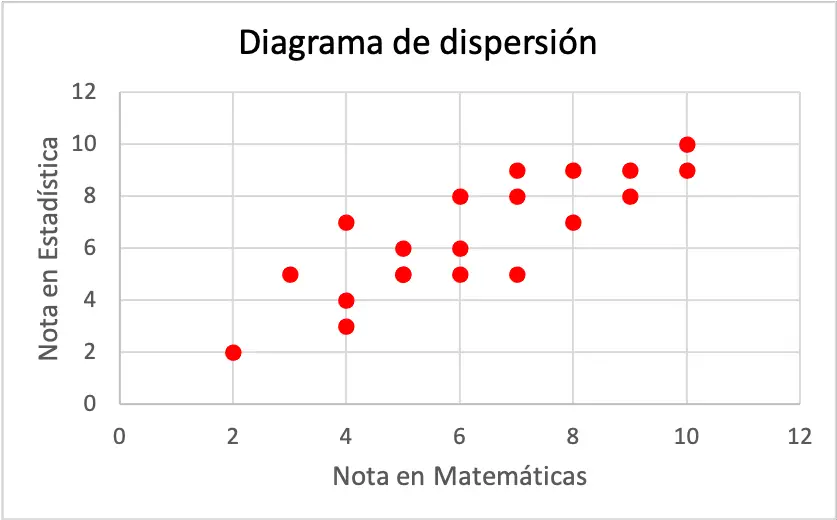
散点图的每个轴代表一个变量。更准确地说，横轴属于数学成绩，而纵轴则对应统计学成绩。

从散点图中可以看出，两个变量呈正相关，因为一个变量随着另一个变量的增加而增加。因此，得出的结论是，如果一个学生在数学上取得更好的成绩，他或她在统计学上也更有可能取得更好的成绩，反之亦然。

然而，前面的结论并不意味着一个变量是另一个变量的原因，因为在数学上取得好成绩并不能自动保证在不做任何事情的情况下在统计学上取得好成绩，而是应该学习这两门科目。在下一节中，我们将更详细地讨论这个概念。

散点图和相关性

从散点图中，可以识别两个变量之间的相关类型：

• 直接相关（或正相关） ：一个变量随着另一个变量的增加而增加。
• 逆相关（或负相关） ：当一个变量增加时，另一个变量减少，反之亦然，如果一个变量减少，另一个变量增加。
• 零相关（无相关） ：两个变量之间没有关系。

同样，无论两个变量之间的相关性是正相关还是反相关，也可以根据两个变量之间关系的强弱对相关性进行分类。

• 强相关性：两个变量密切相关。这些点聚集在点云上。这使得更容易识别变量之间的关系。
• 低相关性：两个变量之间存在关系，但很难识别。点云上的点彼此远离。

另一方面，相关性也可以使用公式进行数值计算，使您可以从数学上了解两个不同变量的相关程度。要查看其工作原理，请单击以下链接：

请记住，即使两个变量之间存在相关性，也不意味着它们之间存在因果关系，即两个变量之间的相关性并不意味着一个变量的变化是另一个变量变化的原因。多变的。

所以，就像上一节的散点图一样，虽然数学成绩和统计成绩之间存在正相关关系，但是数学取得好成绩并不意味着统计取得好成绩，因为如果你只学习数学，你肯定会失败在统计中。因此，这两个变量是相关的，但不是因果关系。

要了解更多信息，您可以继续阅读以下帖子：

点云的优点和缺点

由于散点图的特点，这类统计图表有优点也有缺点。

优势：

• 在散点图上表示一系列数据非常简单。
• 散点图可以让您直观地分析两个变量之间的关系，从而更容易得出结论。
• 散点图还可以用于深入的统计研究，作为初步的数据探索。

缺点：

• 这些类型的图表对于表示定性变量没有用处。
• 解释散点图可能会导致对两个变量之间的因果关系得出错误的结论。
• 散点图不允许您分析两个以上变量之间的关系。