如何在 google 表格中计算偏度和峰度

在统计学中，偏度和峰度是测量分布形状的两种方法。

偏度是分布偏度的度量。该值可以是正值，也可以是负值。

• 负偏度表示尾部位于分布的左侧，向更多负值延伸。
• 正偏度表示尾部位于分布的右侧，向更正的值延伸。
• 值为零表示分布不存在不对称性，这意味着分布完全对称。

峰度是衡量分布与正态分布相比是重尾还是轻尾的指标。

• 正态分布的峰度为 3。
• 如果给定分布的峰度小于 3，则称其为playkurtic ，这意味着与正态分布相比，它往往会产生更少且不太极端的异常值。
• 如果给定分布的峰度大于 3，则称为尖峰分布，这意味着它往往会比正态分布产生更多的异常值。

本教程介绍如何计算 Google 表格中给定数据集的偏度和峰度。

示例：Google 表格中的偏斜和扁平化

假设我们有以下数据集：

为了计算该数据集的偏度和峰度，我们可以使用SKEW()和KURT()函数，语法如下：

• SKEW（值表）
• KURT（数值表）

需要注意的是，任一函数都会返回#DIV/0 错误！在以下两种场景中：

• 如果数据点少于三个。
• 如果样本标准差为零。

下图显示了如何将这些函数用于我们的特定数据集：

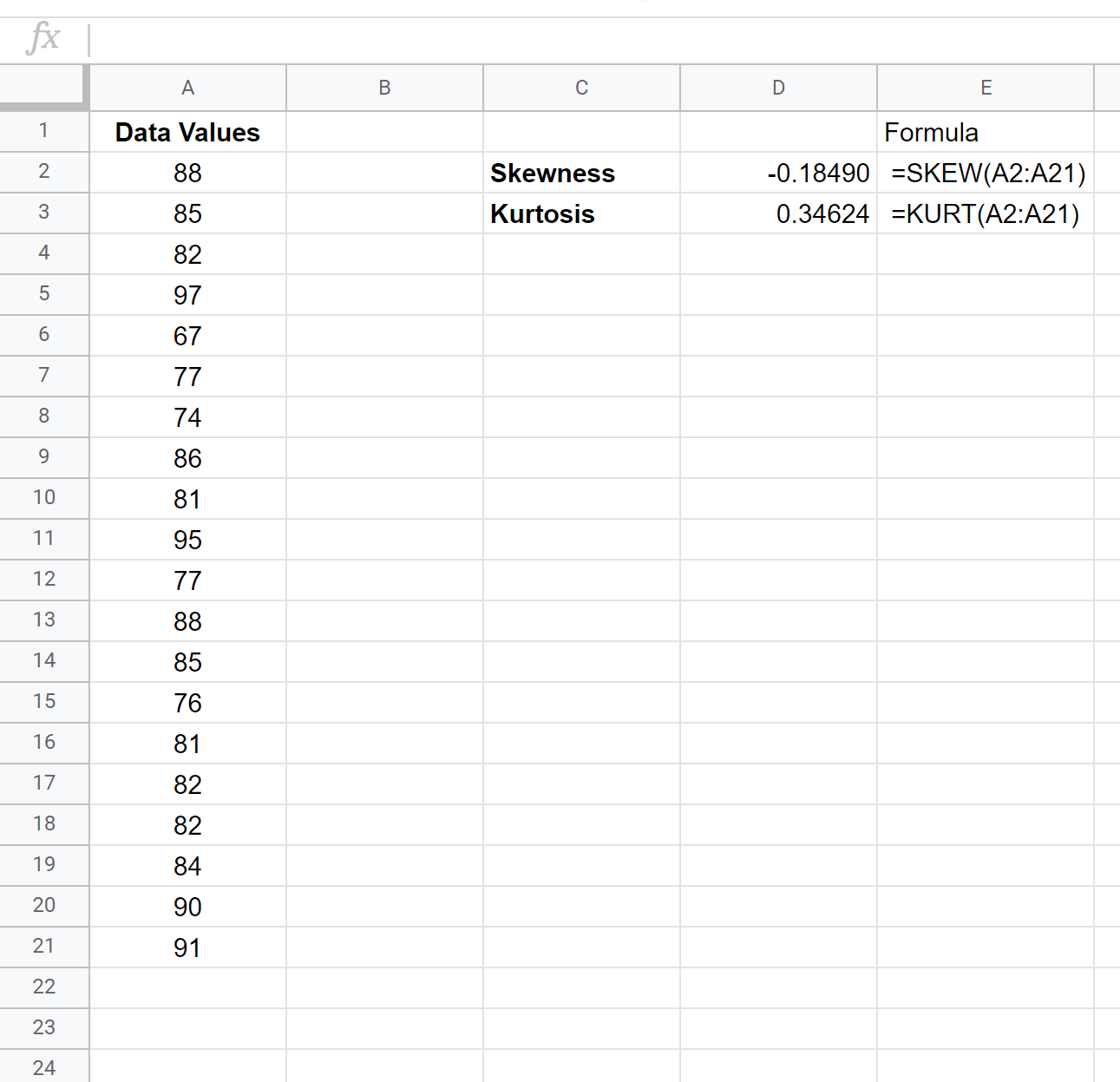
偏度结果为-0.18490 ，峰度结果为0.34624 。

附加资源：偏度和峰度计算器

您还可以使用统计偏度和峰度计算器来计算给定数据集的偏度，该计算器会自动计算给定数据集的偏度和峰度。