如何在 google 表格中执行 t 检验

一般来说，t检验分为三种类型：

• 样本 t 检验
• 两样本 T 检验
• 配对样本 t 检验

本教程提供了如何在 Google 表格中执行每个测试的示例。

示例：单样本 t 检验

定义：单样本 t 检验用于检验总体平均值是否等于某个值。

示例：植物学家想知道某种植物物种的平均高度是否等于 15 英寸。她随机抽取了 12 种植物并记录了每种植物的高度（以英寸为单位）。

以下屏幕截图显示了如何执行单样本 t 检验来确定真实平均人口身高是否等于 15 英寸：

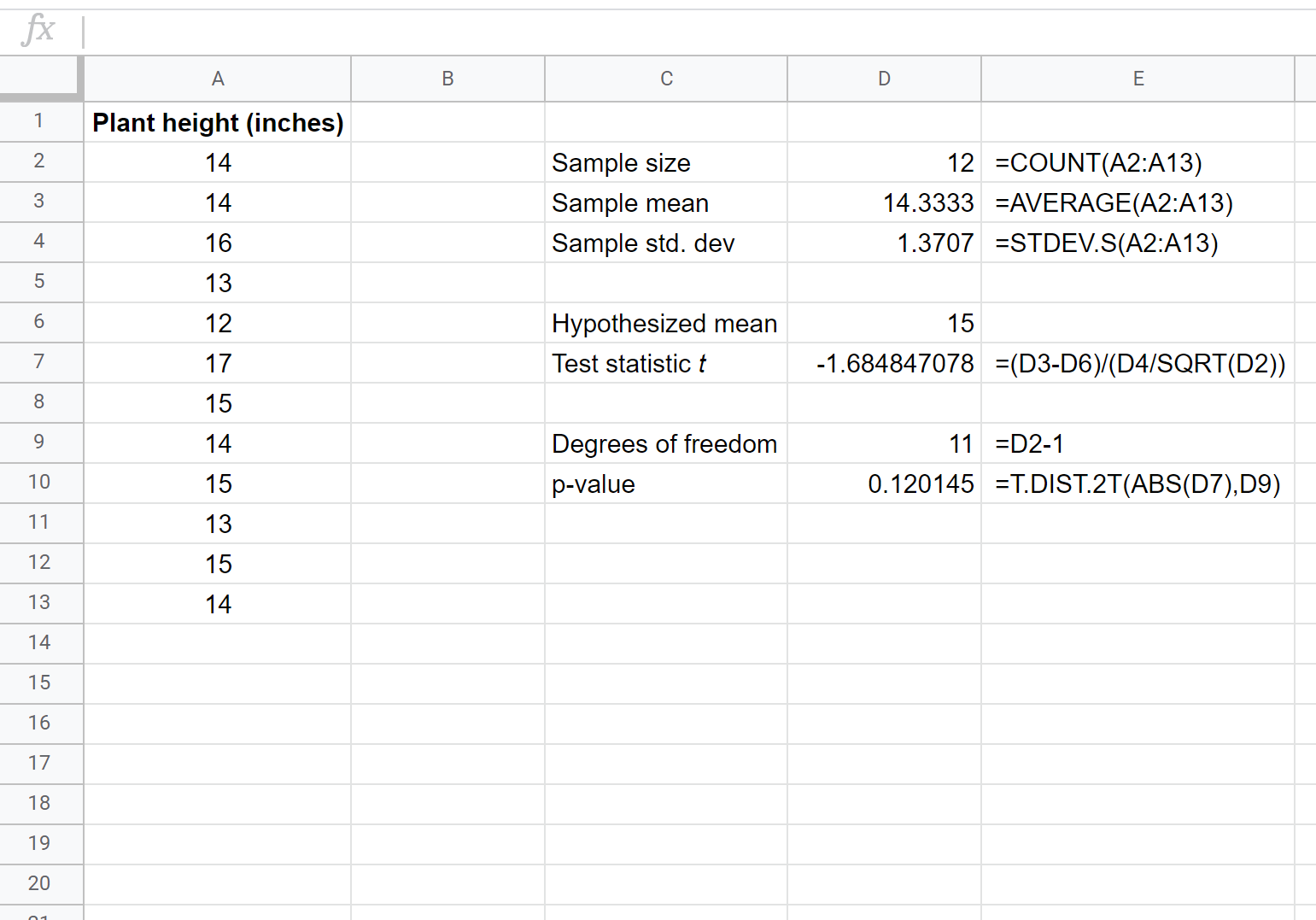
针对特定样本进行 t 检验的两个假设如下：

H ₀ : µ = 15（该植物物种的平均高度为 15 英寸）

H _A : µ ≠15（平均高度不是15 英寸）

我们的检验的 p 值(0.120145)大于 alpha = 0.05，我们无法拒绝检验的原假设。我们没有足够的证据表明这种特定植物的平均高度不是 15 英寸。

示例：双样本 t 检验

定义： 双样本 t 检验用于检验两个总体的均值是否相等。

示例：研究人员想知道某个国家的两种不同植物物种是否具有相同的平均高度。他们从每个物种中随机采集 20 株植物样本，并记录每株植物的高度（以英寸为单位）。

以下屏幕截图显示了如何使用T.TEST()函数执行两个样本 t 检验，以确定两个总体的平均身高是否相等：

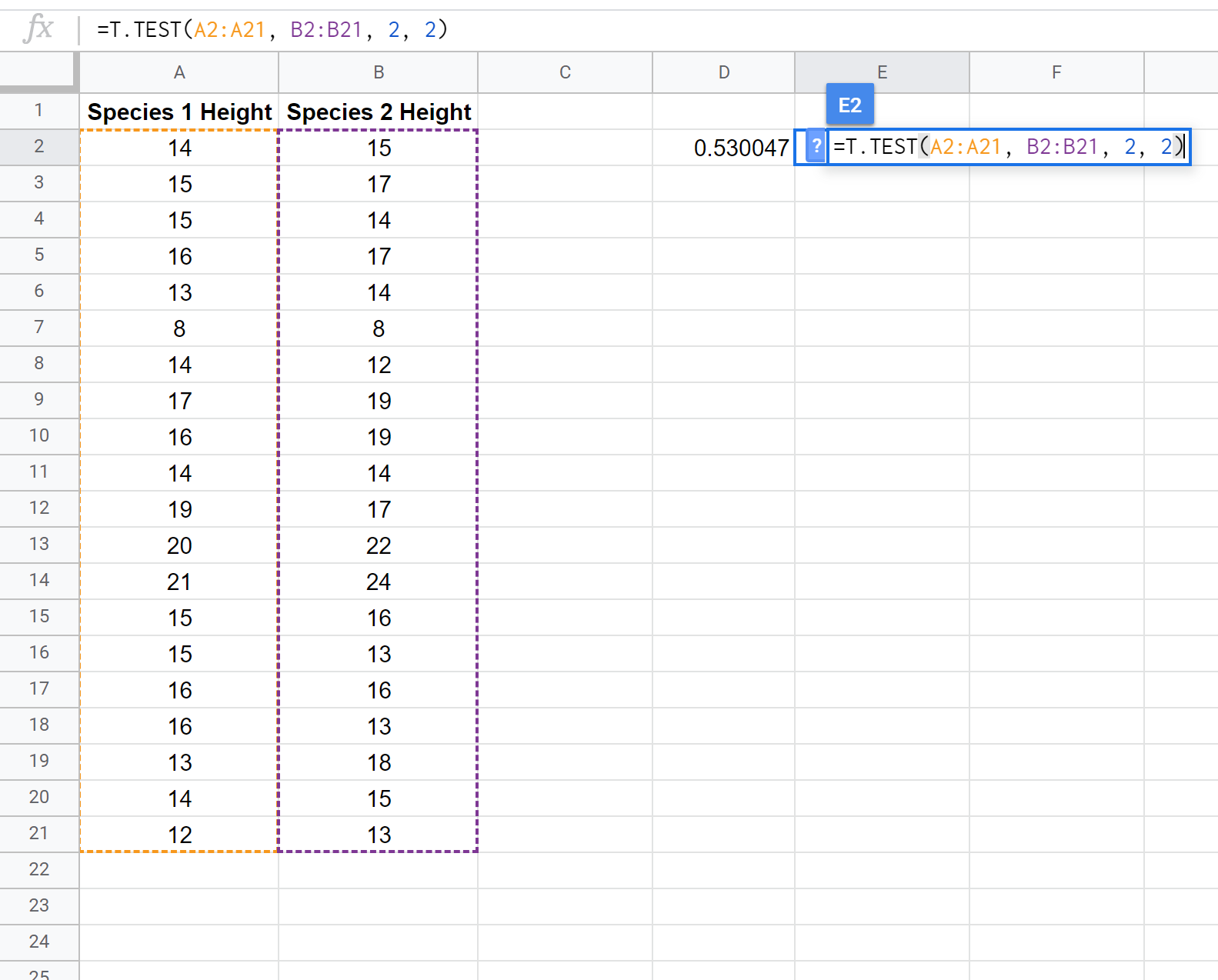
注意：也可以在假设两个样本具有相同方差的情况下执行单尾双样本 t 检验。请参阅T.TEST 文档以了解如何调整测试假设。

此双样本 t 检验的两个假设是：

H ₀ : μ ₁ = μ ₂ （两个总体平均值相等）

H ₁ : μ ₁ ≠ μ ₂ （两个总体平均值不相等）

由于我们的检验的 p 值(0.530047)大于 alpha = 0.05，因此我们无法拒绝检验的原假设。我们没有足够的证据表明这种特定植物的平均高度不是 15 英寸。

示例：配对样本 t 检验

定义：当一个样本的每个观察值可以与另一个样本的观察值相关时 ，配对样本 t 检验用于比较两个样本的平均值。

示例：我们想知道一门学习课程是否对学生在特定考试中的表现有重大影响。为了测试这一点，我们要求一个班级 20 名学生进行预测试。然后我们让每个学生参加为期两周的课程。然后，学生重新参加类似难度的测试。

以下屏幕截图显示了如何执行配对样本 t 检验来比较第一次和第二次测试的平均分数之间的差异：

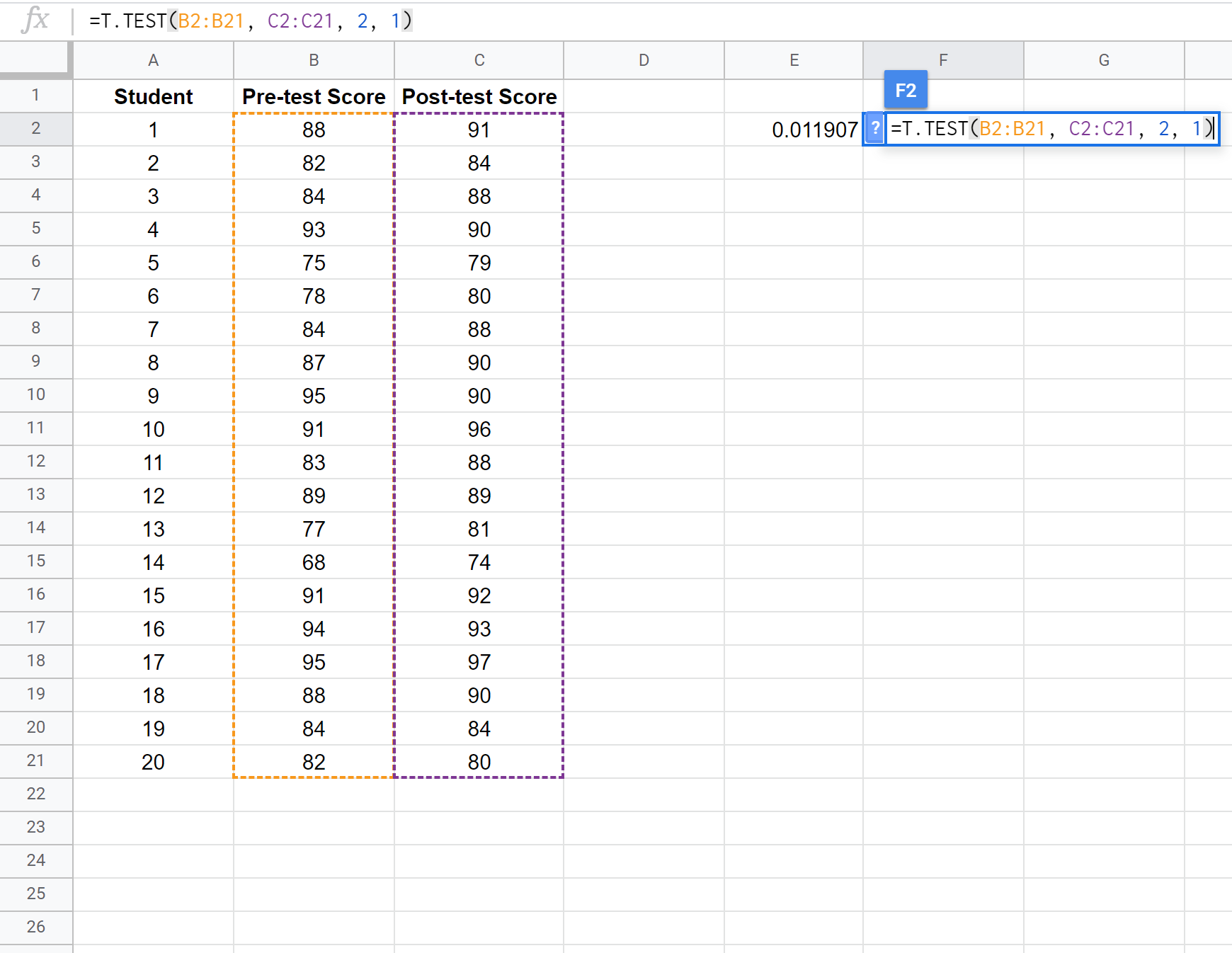
注意：也可以在假设两个样本具有相同方差的情况下执行单尾双样本 t 检验。请参阅T.TEST 文档以了解如何调整测试假设。

此配对样本 t 检验的两个假设是：

H ₀ : μ ₁ = μ ₂ （两个总体平均值相等）

H ₁ : μ ₁ ≠ μ ₂ （两个总体平均值不相等）

由于我们的检验的 p 值(0.011907)小于 alpha = 0.05，因此我们拒绝检验的原假设。我们有足够的证据表明，测试前和测试后的平均分数之间存在统计上的显着差异。