如何在 r 中执行相关性测试（附示例）

量化两个变量之间关系的一种方法是使用Pearson 相关系数，它是两个变量之间线性关联的度量。

它始终采用 -1 和 1 之间的值，其中：

• -1 表示两个变量之间完全负线性相关
• 0 表示两个变量之间不存在线性相关
• 1 表示两个变量之间存在完全正线性相关

要确定相关系数是否具有统计显着性，您可以计算相应的 t 分数和 p 值。

相关系数 (r) 的 t 分数计算公式为：

t = r * √ n-2 / √ 1-r ²

p 值计算为具有 n-2 自由度的 t 分布的相应双尾 p 值。

示例：R 中的相关性测试

要确定两个变量之间的相关系数是否具有统计显着性，您可以使用以下语法在 R 中执行相关性测试：

cor.test(x, y, method=c(“pearson”, “kendall”, “spearman”))

金子：

• x，y：数字数据向量。
• method：用于计算两个向量之间相关性的方法。默认为“皮尔逊”。

例如，假设 R 中有以下两个向量：

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

在对两个变量之间进行相关性测试之前，我们可以创建一个快速散点图来可视化它们的关系：

 #create scatterplot
plot(x, y, pch= 16 )

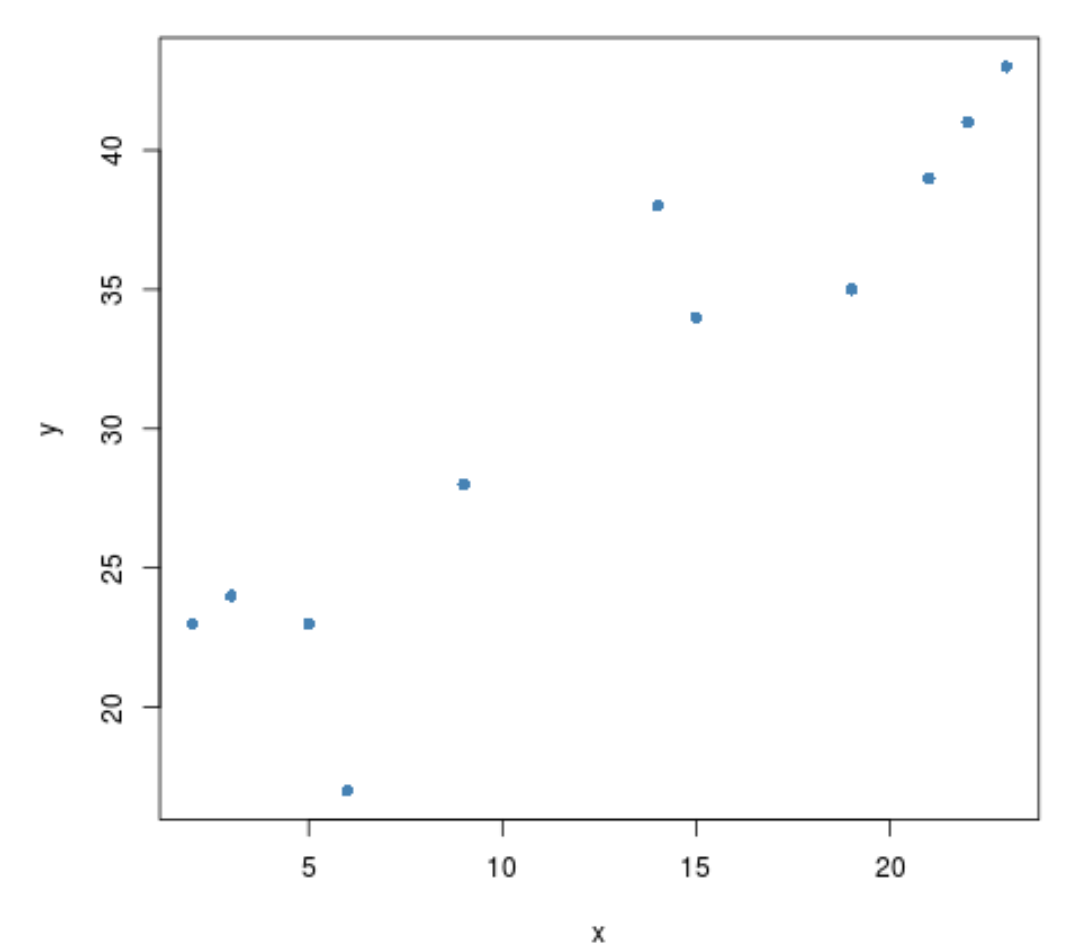
这两个变量之间似乎存在正相关关系。也就是说，随着其中一个的增加，另一个也趋于增加。

为了查看这种相关性是否具有统计显着性，我们可以执行相关性测试：

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

两个向量之间的相关系数为0.9279869 。

检验统计量结果为7.8756 ，相应的 p 值为1.35e-05 。

由于该值小于 0.05，我们有足够的证据表明两个变量之间的相关性具有统计显着性。

其他资源

以下教程提供有关相关系数的其他信息：

皮尔逊相关系数简介
什么被认为是“强”相关性？
皮尔逊相关性的五个假设