概率函数

本文解释什么是概率函数。因此，您将了解概率函数的含义、其属性以及计算概率函数的具体示例。此外，还介绍了概率函数与其他类型的概率函数之间的差异。

什么是概率函数？

概率函数，也称为概率质量函数，是描述离散随机变量取特定值的概率的数学函数。

也就是说，概率函数返回与离散变量完全等于某个值相关的概率。

例如，掷骰子时掷出任何数字的概率是 1/6（骰子有六个面），因此无论 n 为什么值，与此样本空间相关的概率函数都将等于 1/6。

概率函数的性质

概率函数具有以下属性：

• 概率不能为负，因此对于任何 x 值，概率函数为零或正。

• 同样，最大概率是统一的，这意味着该事件总是会发生。因此，概率函数的最大值等于1。

• 最后，概率函数所有值的总和为 1，因为它是样本空间中所有概率的总和。

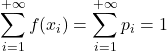
概率函数示例

现在我们知道了概率函数的定义和特征，让我们看一个此类概率函数的示例。

• 通过四次独立的抛硬币来计算获得 0、1、2、3 和 4 次正面朝上的概率。接下来，绘制找到的概率函数的图表。

首先，我们必须计算获得正面的概率，为此，我们必须将可能的情况除以情况总数。您可以在下表中看到所有概率的计算：

一旦我们计算出了所有的概率，我们就可以在图上表示概率函数的值：

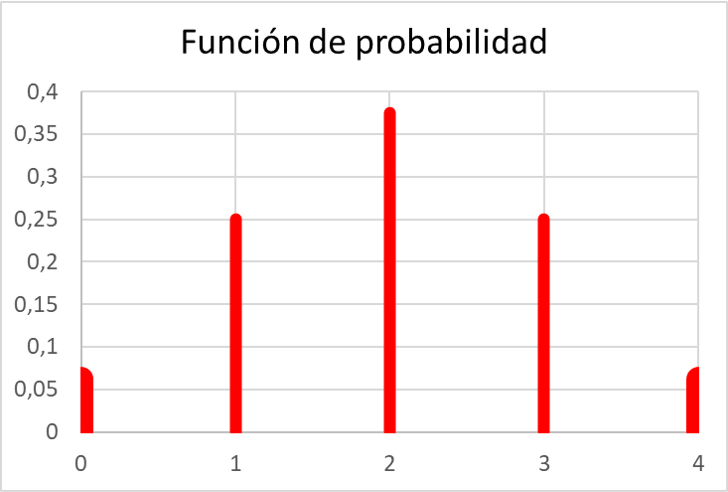
正如您所看到的，练习中的概率函数满足概率函数的所有属性，因为它的所有值都在 0 和 1 之间，而且它的所有值的总和等于 1。

概率函数和密度函数

在本节中，我们将看到概率函数和密度函数之间的区别，因为它们是具有相同目的但在不同情况下使用的两种类型的概率函数。

概率函数和密度函数之间的区别在于概率描述的变量类型。概率函数用于定义离散变量的概率，而密度函数用于定义连续变量的概率。

因此，根据变量，使用概率函数或密度函数。

要了解有关密度函数的更多信息，请单击以下链接：

概率函数和分布函数

概率函数和分布函数之间的区别在于它们定义的概率类型。概率函数表示变量取某一值的概率，而分布函数描述变量的累积概率。

因此，分布函数是根据概率函数计算出来的。

例如，在下面的链接中，您可以看到基于上面练习中找到的概率函数，计算从四次抛硬币中获得正面的分布函数。