多项式回归简介

当我们有一个包含预测变量和响应变量的数据集时，我们经常使用简单线性回归来量化两个变量之间的关系。

然而，简单线性回归 (SLR) 假设预测变量和响应变量之间的关系是线性的。用数学符号表示，SLR 假设该关系采用以下形式：

Y = β ₀ + β ₁ X + ε

但实际上，两个变量之间的关系实际上可能是非线性的，尝试使用线性回归可能会导致模型拟合不佳。

解释预测变量和响应变量之间非线性关系的一种方法是使用多项式回归，其形式为：

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

在此方程中， h称为多项式的次数。

当我们增加h的值时，模型能够更好地适应非线性关系，但在实践中我们很少选择h大于 3 或 4。超过这一点，模型就会变得过于灵活并且过度拟合数据。

技术说明

• 尽管多项式回归可以拟合非线性数据，但它仍然被视为线性回归的一种形式，因为它的系数_β1 、 _β2 、 …、 _βh是线性的。
• 多项式回归也可用于多个预测变量，但这会在模型中创建交互项，如果使用多个预测变量，则可能会使模型变得极其复杂。

何时使用多项式回归

当预测变量和响应变量之间的关系是非线性时，我们使用多项式回归。

检测非线性关系有三种常见方法：

1. 创建散点图。

检测非线性关系的最简单方法是创建响应变量与预测变量的散点图。

例如，如果我们创建以下散点图，我们可以看到两个变量之间的关系近似线性，因此简单的线性回归可能对该数据表现良好。

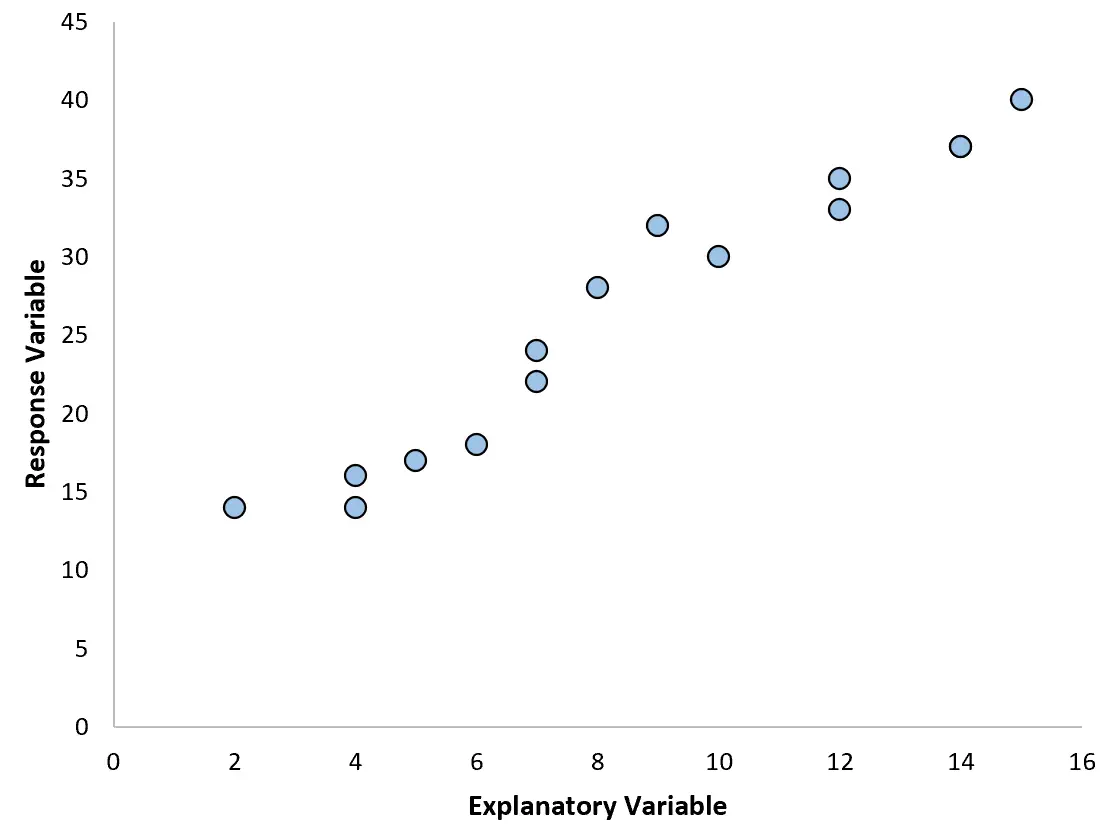
但是，如果我们的散点图类似于以下图表之一，我们可能会发现该关系是非线性的，因此多项式回归将是一个好主意：

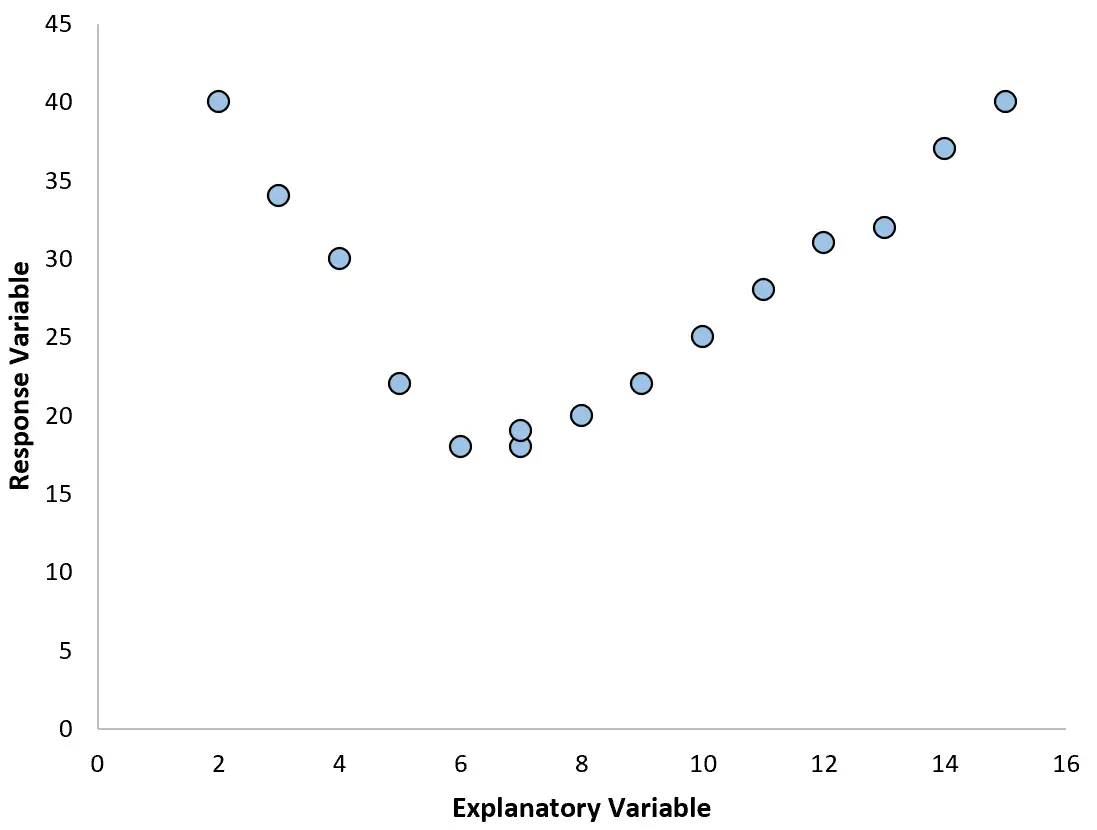
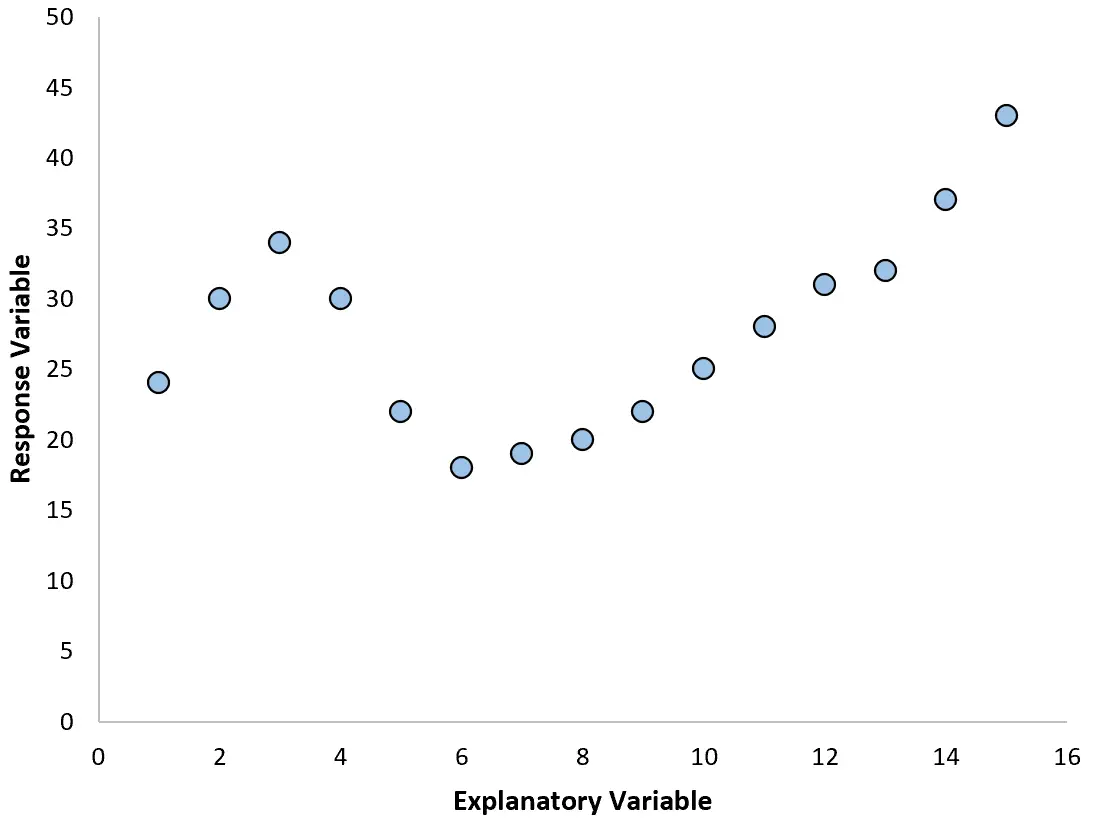
2. 根据拟合图创建残差图。

检测非线性的另一种方法是对数据拟合一个简单的线性回归模型，然后生成残差与拟合值的关系图。

如果图残差大致均匀地分布在零附近，没有明显的趋势，则简单的线性回归可能就足够了。

但是，如果残差在图中显示非线性趋势，则表明预测变量和响应之间的关系可能是非线性的。

3. 计算模型的R ² 。

回归模型的 R ²值告诉您可以由预测变量解释的响应变量的变化百分比。

如果您将简单的线性回归模型拟合到数据集并且模型的 R ²值非常低，则这可能表明预测变量和响应变量之间的关系比简单的线性关系更复杂。

这可能表明您可能需要尝试多项式回归。

相关： 什么是好的 R 平方值？

如何选择多项式的次数

多项式回归模型采用以下形式：

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

在此等式中， h是多项式的次数。

但如何选择h的值呢？

在实践中，我们用不同的h值拟合几个不同的模型，并执行k 倍交叉验证，以确定哪个模型产生最低的测试均方误差 (MSE)。

例如，我们可以将以下模型拟合到给定的数据集：

• Y = β ₀ + β ₁
• Y = β ₀ + β ₁ X + β ₂ X ²
• ^{Y =} _β0 + _β1X + _β2X2 + _β3X3
• Y = β ₀ + β ₁ X + β ₂ X ² + β ₃ X ³ + β ₄ X ⁴

然后，我们可以使用 k 折交叉验证来计算每个模型的 MSE 测试，这将告诉我们每个模型在以前从未见过的数据上的表现如何。

多项式回归的偏差-方差权衡

使用多项式回归时存在 偏差-方差权衡。当我们增加多项式的次数时，偏差会减小（因为模型变得更加灵活），但方差会增加。

与所有机器学习模型一样，我们需要在偏差和方差之间找到最佳权衡。

在大多数情况下，这允许多项式的次数在一定程度上增加，但超过某个值后，模型开始适应数据中的噪声，并且测试的 MSE 开始下降。

为了确保我们拟合的模型既灵活又不太灵活，我们使用 k 折交叉验证来查找产生最低 MSE 测试的模型。

如何执行多项式回归

以下教程提供了如何在不同软件中执行多项式回归的示例：

如何在 Excel 中执行多项式回归
如何在 R 中执行多项式回归
如何在 Python 中执行多项式回归