手动多元线性回归（一步一步）
多元线性回归是一种可以用来量化两个或多个预测变量与响应变量之间关系的方法。
本教程说明如何手动执行多元线性回归。
示例：手动多元线性回归
假设我们有以下数据集，其中包含一个响应变量y和两个预测变量 x 1和 x 2 ：
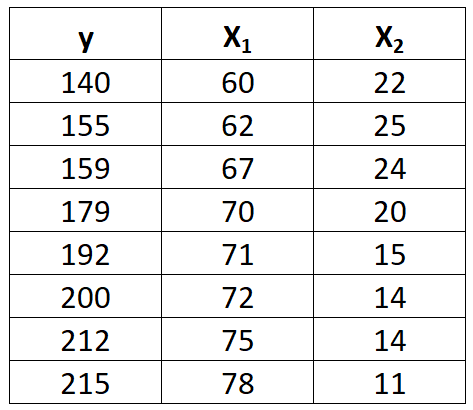
完成以下步骤以拟合该数据集的多元线性回归模型。
步骤1：计算x 1 2 、x 2 2 、x 1 y、x 2 y 和x 1 x 2 。
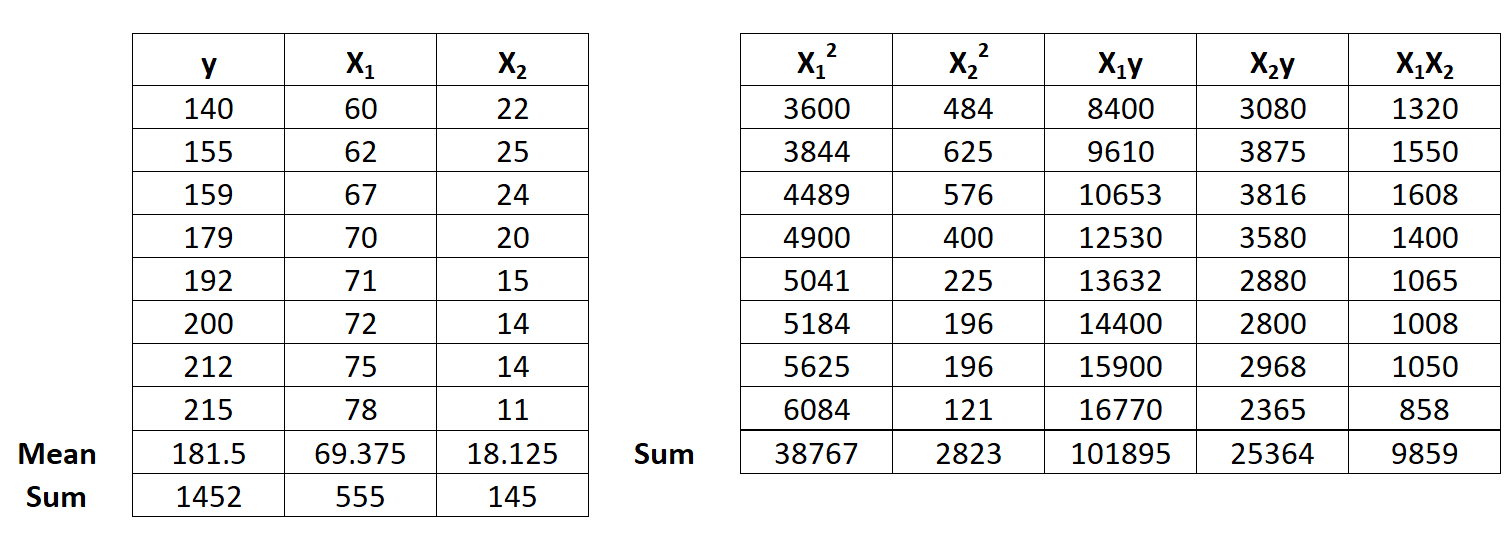
步骤 2：计算回归和。
接下来，执行以下回归和计算：
- Σx12 = ΣX12 – ( ΣX1 ) 2 / n = 38.767 – (555) 2 / 8 = 263.875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / n = 2823 – (145) 2 / 8 = 194.875
- Σ x 1 y = Σ
- Σ x 2 y = Σ
- Σ x 1 x 2 = Σ
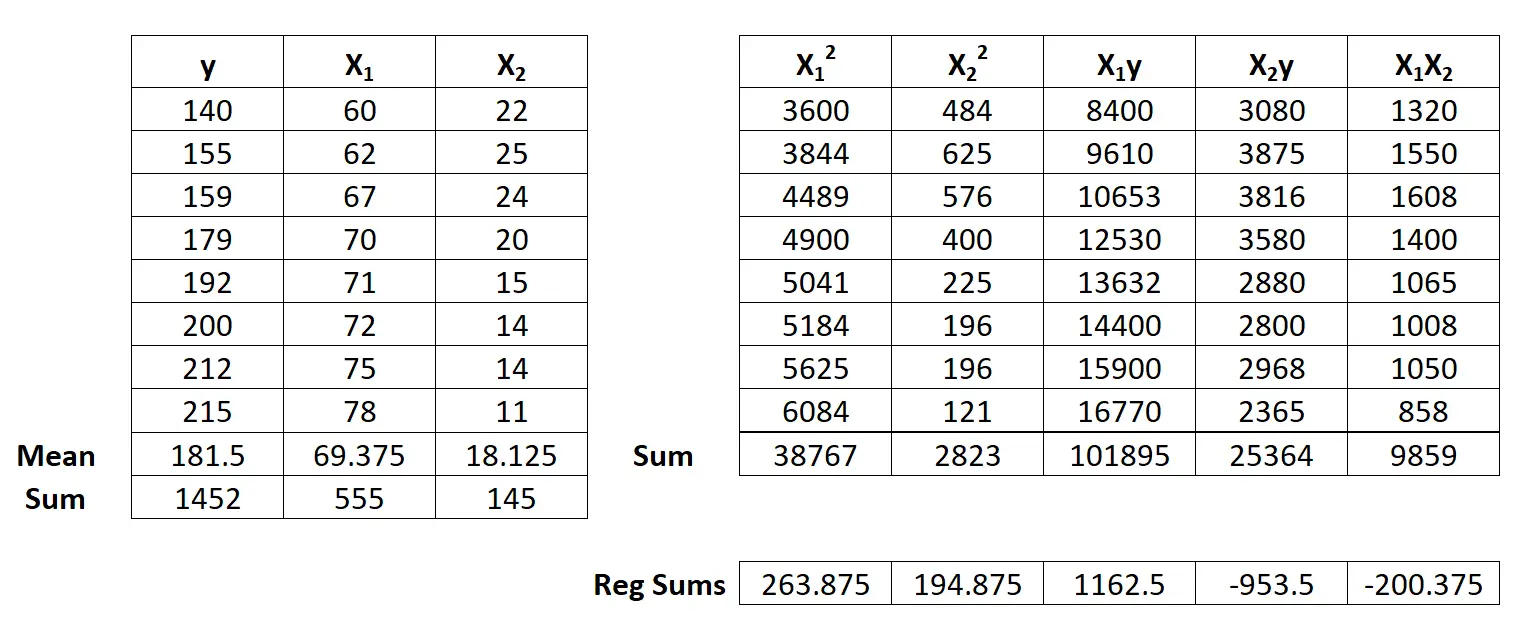
步骤3：计算b 0 、b 1和b 2 。
b 1的计算公式为： [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
因此， b 1 = [(194.875)(1162.5) – (-200.375)(-953.5)] / [(263.875) (194.875) – (-200.375) 2 ] = 3.148
b 2的计算公式为： [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
因此， b 2 = [(263.875)(-953.5) – (-200.375)(1152.5)] / [(263.875) (194.875) – (-200.375) 2 ] = -1.656
b 0的计算公式为： y – b 1 X 1 – b 2 X 2
因此， b 0 = 181.5 – 3.148(69.375) – (-1.656)(18.125) = -6.867
步骤5：将b 0 、b 1和b 2代入估计的线性回归方程。
估计的线性回归方程为： ŷ = b 0 + b 1 *x 1 + b 2 *x 2
在我们的示例中，它是ŷ = -6.867 + 3.148x 1 – 1.656x 2
如何解释多元线性回归方程
以下是如何解释这个估计的线性回归方程： ŷ = -6.867 + 3.148x 1 – 1.656x 2
b0 = -6.867 。当两个预测变量都等于 0 时，y 的平均值为 -6.867。
b1 = 3.148 。假设 x 2保持不变，平均而言，x 1增加 1 个单位与 y 增加 3.148 个单位相关。
b2 = -1.656 。假设 x 1 保持不变，x 2增加 1个单位平均意味着 y 减少 1,656 个单位。
其他资源
多元线性回归简介
如何手动执行简单线性回归
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多