正态分布和 t 分布：有什么区别？

正态分布是所有统计中最常用的分布，众所周知，它是对称的、钟形的。

一个密切相关的分布是t 分布，它也是对称的、钟形的，但它的“尾巴”比正态分布更重。

换句话说，与正态分布相比，分布中位于末端的值多于位于中心的值：

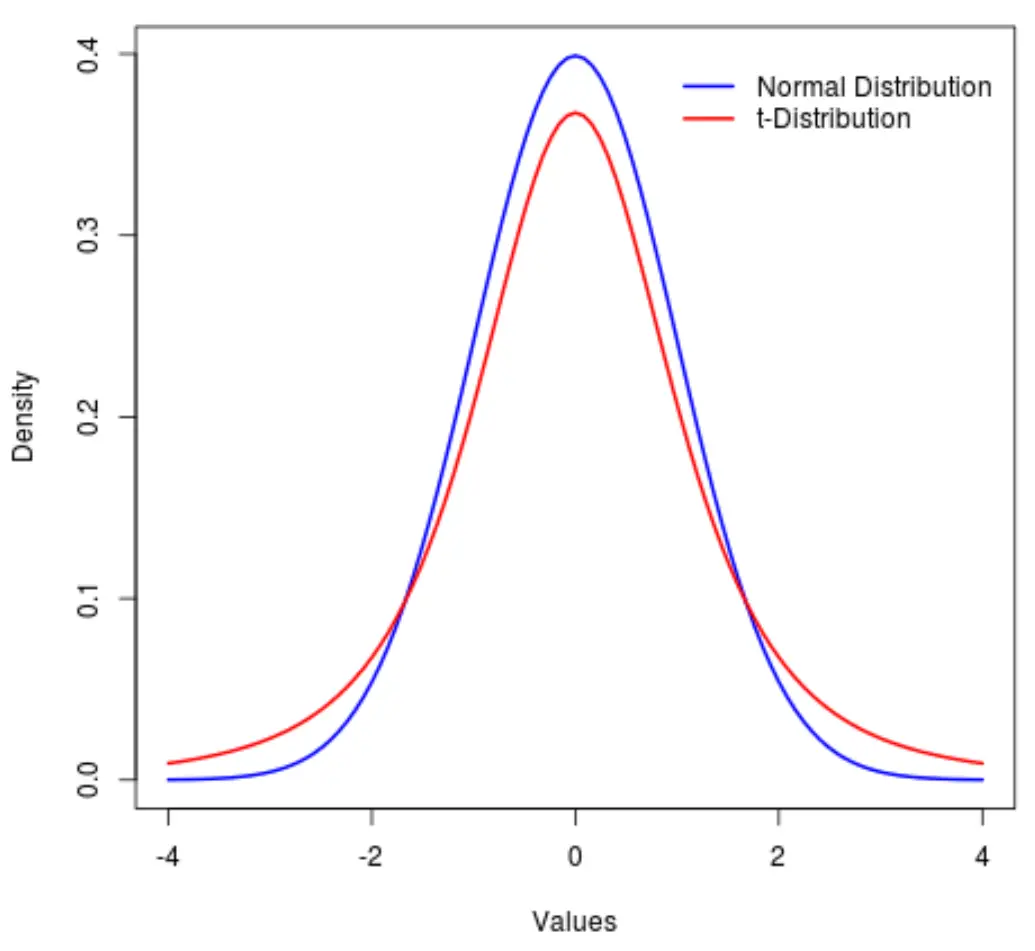
用统计术语来说，我们使用一种称为峰度的指标来衡量分布的“重度”。因此，我们可以说 t 分布的峰度大于正态分布的峰度。

在实践中，我们在执行假设检验或构建置信区间时最常使用 t 分布。

例如，计算总体平均值的置信区间的公式为：

置信区间 = x +/- t _{1-α/2, n-1} *(s/√ n )

金子：

• x ：样本平均值
• t：临界 t 值，基于显着性水平α和样本大小n
• s：样本标准差
• n：样本量

在此公式中，当满足以下条件之一时，我们使用表 t 的临界值代替表 z 的临界值：

• 我们不知道总体标准差。
• 样本量小于或等于30。

以下流程图提供了一种有用的方法来了解是否应该使用表 t 或表 z 中的临界值：

在构建置信区间时使用t分布和使用正态分布的主要区别在于t分布的临界值会更大，导致置信区间更宽。

例如，假设我们要为海龟种群的平均体重构建 95% 的置信区间，以便收集具有以下信息的海龟随机样本：

• 样本量n = 25
• 平均样本重量x = 300
• 样本标准差s = 18.5

95% 置信水平的临界 z 值为1.96 ，而 df = 25-1 = 24 自由度的 95% 置信区间的临界 t 值为2.0639 。

因此，使用 z 临界值的总体平均值的 95% 置信区间为：

95% CI = 300 +/- 1.96*(18.5/√ 25 ) = [292.75, 307.25]

而使用 t 临界值的总体平均值的 95% 置信区间为：

95% CI = 300 +/- 2.0639*(18.5/√25) = [292.36, 307.64]

请注意，t 临界值的置信区间更宽。

这里的想法是，当我们的样本量较小时，我们不太确定真实的总体平均值，因此使用 t 分布来生成更宽的置信区间很有用，这样更有可能包含真实的总体平均值。

t 分布自由度的可视化

需要注意的是，随着自由度的增加，t 分布接近正态分布。

为了说明这一点，请考虑下图，它显示了具有以下自由度的 t 分布的形状：

• df = 3
• df = 10
• df = 30

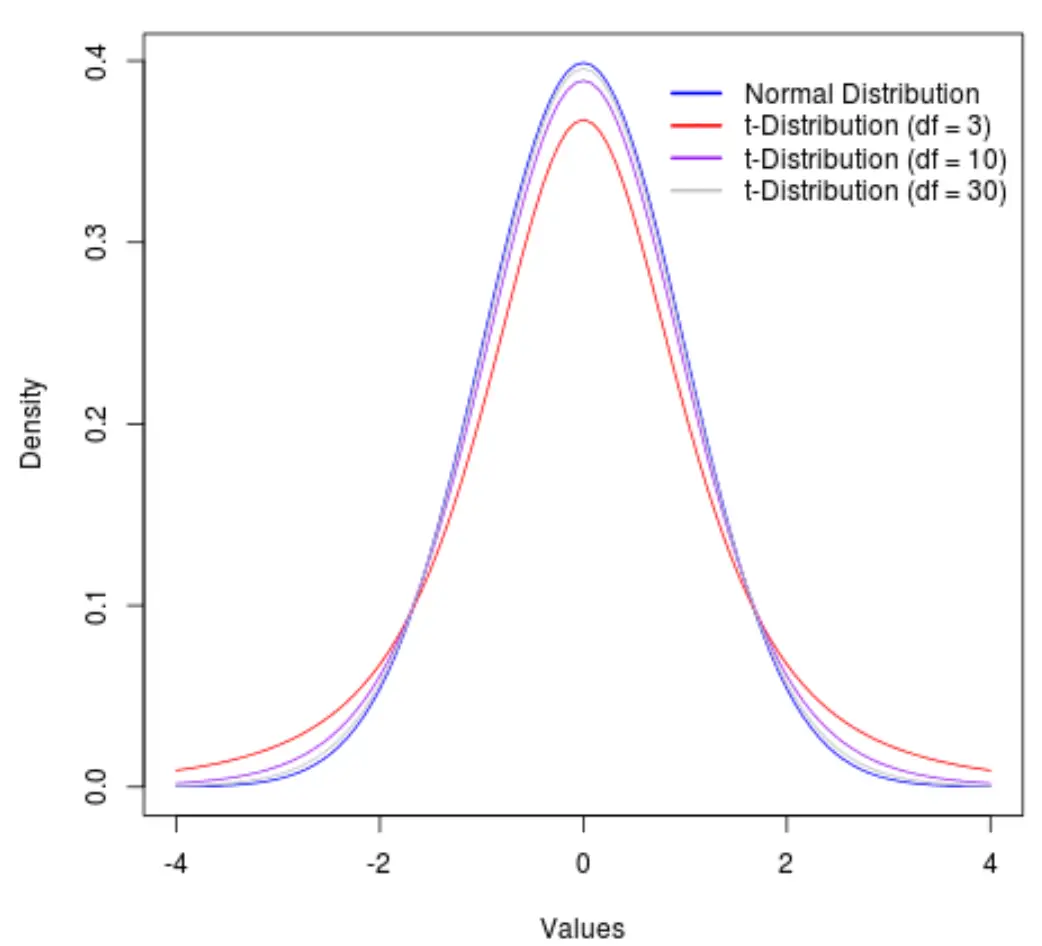
自由度超过 30 度后，t 分布和正态分布变得非常相似，以至于在公式中使用 t 临界值和 z 临界值之间的差异可以忽略不计。