绝对平均偏差与标准偏差：有什么区别？

标准差是衡量数据集分布的最常见方法之一。

计算方法如下：

标准差 = √( Σ( _xi – x ) ² / n )

衡量数据集中观测值分布的另一种方法是平均绝对偏差。

计算方法如下：

平均绝对偏差 = Σ|x _i – x | /不是

本教程解释了这两个指标之间的差异以及如何计算每个指标的示例。

共同点和不同点

顾名思义，标准偏差和平均绝对偏差试图量化给定数据集中观测值与平均值的典型偏差。

然而，每个指标使用的方法是不同的。

标准差

标准差求出每个观测值与数据集平均值之间的平方差。然后对这些平方差进行平均并取平方根。

这给我们留下了一个代表观察值与平均值的“标准”或典型偏差的数字。

表示绝对偏差

相反，平均绝对偏差是指每个观测值与数据集平均值之间的绝对偏差。然后找到这些偏差的平均值。

这给我们留下了一个代表观测值与平均值的平均偏差的数字。

由于标准差求平方差，因此它始终等于或大于平均绝对偏差。

当存在极端异常值时，标准偏差将远大于平均绝对偏差。下面的例子说明了这一点。

示例：标准偏差的平均绝对偏差

假设我们有以下 8 个值的数据集：

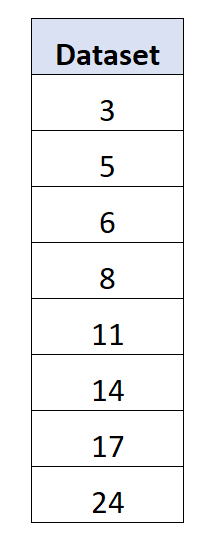
结果平均值是11 。

因此，我们将计算平均绝对偏差如下：

平均绝对偏差= (|3-11| + |5-11| + |6-11| + |8-11| + |11-11| + |14-11| + |17-11| + |24- 11|) / 8 = 5.5 。

我们将计算标准差如下：

标准差 = √((3-11) ² + (5-11) ² + (6-11) ² + (8-11) ² + (11-11) ² + (14-11) ² + (17- 11) ² + (24-11) ² )/8) = 6.595 。

如前所述，标准偏差始终等于或大于平均绝对偏差。

然而，如果数据集中存在极端异常值，标准差和平均绝对差之间的差异就会特别大。

例如，考虑以下数据集，最后一个值具有极端异常值：

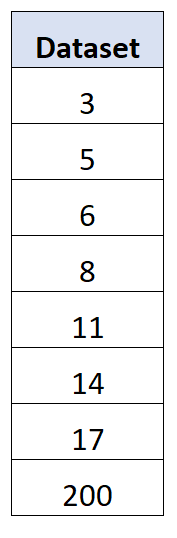
事实证明，该数据集的标准偏差为63.27 ，而平均绝对偏差为41.75 。

极端异常值导致标准差远大于平均绝对差。