标准有效性的简单解释
标准有效性是指一个变量的测量预测另一个变量的响应的能力。
例如,我们可能想知道某些大学入学考试能够在多大程度上预测学生第一学期的平均成绩。
入学考试是解释变量,标准变量是第一学期的 GPA。
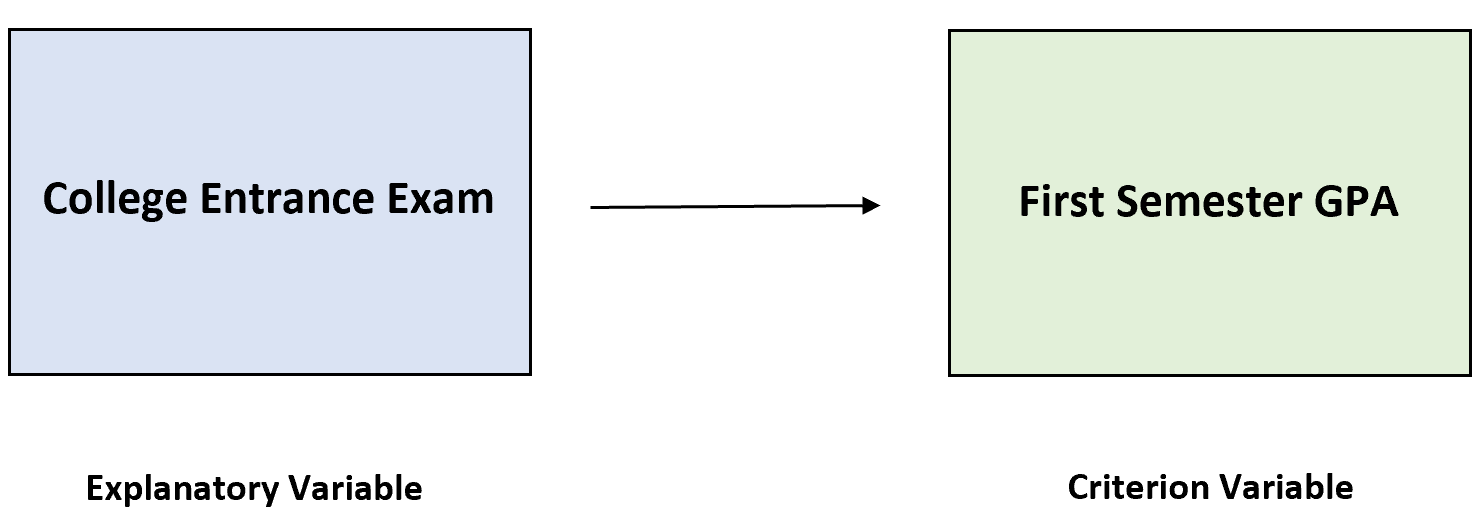
我们想知道使用这个特定的解释变量作为预测标准变量的手段是否有效。
如何衡量标准有效性
我们通常使用皮尔逊相关系数等指标来衡量标准有效性,该系数的值介于 -1 和 1 之间,其中:
- -1 表示两个变量之间完全负线性相关
- 0 表示两个变量之间不存在线性相关
- 1 表示两个变量之间存在完全正线性相关
相关系数距离零越远,两个变量之间的关联性越强。
例如,如果我们收集了 1,000 名学生的入学考试成绩和第一学期 GPA 数据,发现两个变量之间的相关性为0.843 ,这意味着这两个变量高度相关。
换句话说,入学考试成绩高的学生在第一学期也往往会取得高分。相反,入学考试成绩较低的学生在第一学期的 GPA 往往较低。
标准有效性的类型
标准有效性有两种主要类型:
1.预测有效性
第一类标准有效性称为预测有效性,它决定了变量的测量是否能够准确地预测变量未来的测量。
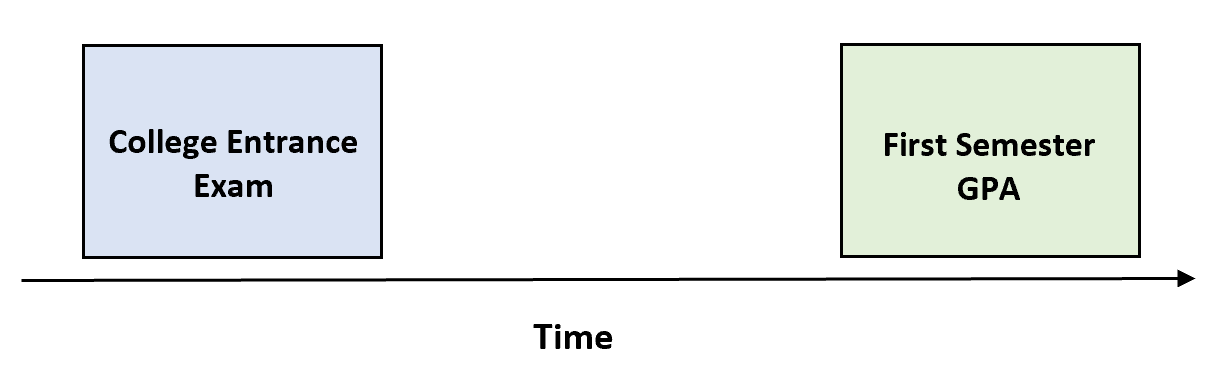
前面测量学生高考成绩和第一学期 GPA 的示例是测量预测有效性的示例,因为我们在不同时间测量这两个变量。
换句话说,我们试图确定入学考试成绩是否可以很好地预测第一学期的GPA。
2、同时有效
第二种类型的标准有效性称为并发有效性,它同时(即同时)测量两个变量以查看一个变量是否与另一个变量显着相关。
一个例子是,如果一家公司进行某种类型的测试,看看测试结果是否与员工的生产力相关。
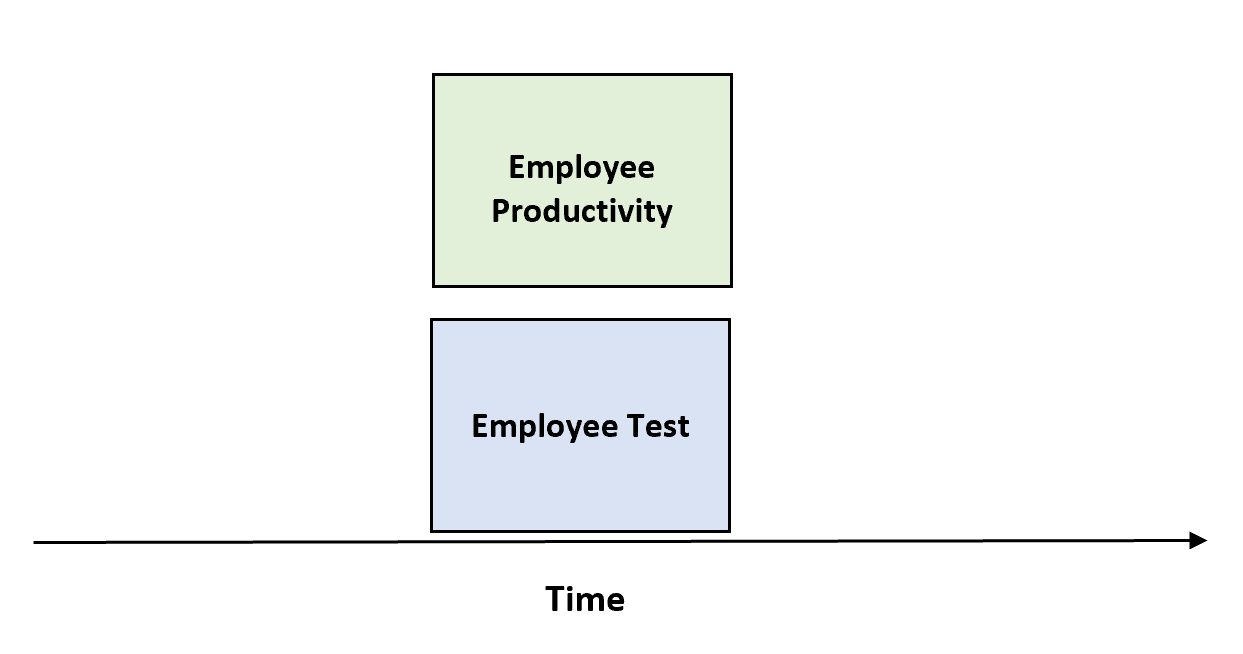
这种方法的优点是我们不需要等待未来一段时间才能对感兴趣的变量标准进行测量。