打字
本文解释了统计中分布特征的含义。因此,您将找到典型化的定义、变量典型化的示例,此外,您将能够通过逐步解决的练习进行练习。
什么是打字?
在统计学中,归一化是对分布应用线性变换,使其平均值和标准差分别等于 0 和 1 的过程。
更准确地说,打字涉及从随机变量中减去平均值,然后除以标准差。
打字也可以称为规范化或标准化。
输入公式
要对变量进行分类,必须减去其平均值,然后除以标准差。因此,输入变量的公式如下:
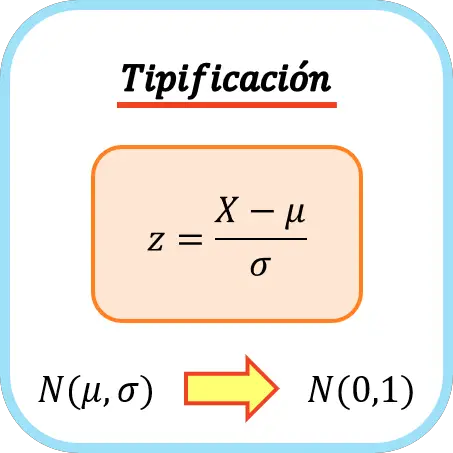
金子
![]()
是变量的平均值
![]()
和
![]()
其标准差(或标准差)。
因此,该条目实际上是变量更改,因为对变量应用了线性变换。
示例条目
考虑到典型化的定义及其公式,下面是一个具体的例子来充分理解这个概念。
- 连续随机变量服从均值 45、标准差 10 的正态分布,获得小于或等于 60 的值的概率是多少?
![]()
为了找到正态分布的概率,我们需要使用它的特征表,但要做到这一点,我们需要首先执行打字过程。因此,我们减去平均值并除以标准差得到概率值:
![]()
标准化后,我们将继续查看正态分布概率表,看看 1.5 的值对应的概率是多少:

从正态分布典型表中可以看出,上一步计算出的值对应的概率如下:
![]()
因此,获得等于或小于 60 的值的概率为 93.32%。
打字练习已解决
计算均值和标准差分别为 120 和 50 的正态分布的以下概率。
![]()
- 获得小于或等于 208 的值的概率。
- 获得大于 137 的值的概率。
在问题的两个部分中,我们都需要输入正态分布来计算概率。
我们首先计算输入小于或等于 208 的值的概率:
![]()
现在让我们看一下上表,值 1.76 对应的概率是多少:
![]()
其次,我们将计算获得大于 137 的值的概率。以同样的方式,我们首先输入变量:
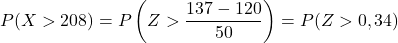 然而,附表只有最低的累积概率,因此要使用该表,我们必须首先转换概率:
然而,附表只有最低的累积概率,因此要使用该表,我们必须首先转换概率:
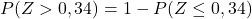 最后,我们将从附表中记下与 Z 的计算值相对应的概率:
最后,我们将从附表中记下与 Z 的计算值相对应的概率:
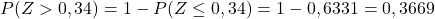
打字有什么意义?
为了完全理解典型化的含义,我们将了解它的用途以及何时必须对变量进行类型化。
标准化主要用于比较具有不同均值和方差的分布值。同样,标准化也用于计算概率。
通过对具有不同特征的分布的两个值进行标准化,我们可以看到哪个值相对于整个分布更大或更小。或者换句话说,通过应用典型化过程,我们可以看到哪个值与其分布的平均值最接近或最远。
此外,如上所述,典型化还允许计算概率,因为概率表通常基于典型分布。