切比雪夫定理

本文解释什么是切比雪夫定理。在这里您可以找到切比雪夫定理公式、已解决的练习，此外还有在线切比雪夫定理计算器。最后说明了切比雪夫定理与经验法则的区别。

什么是切比雪夫定理？

切比雪夫定理，也称为切比雪夫不等式，是一种统计规则，用于计算随机变量的值与其平均值在一定距离内的概率。

换句话说，在统计学中，切比雪夫定理用于确定某个值位于置信区间内的概率。

此外，切比雪夫定理还用于证明其他统计定理，例如大数定律。

虽然切比雪夫定理最初是由法国人 Irénée-Jules Bienaymé 提出的，但该定理之所以如此命名，是因为它是由俄罗斯人帕夫努蒂·切布什夫于 1867 年提出的。

切比雪夫定理的公式

切比雪夫定理指出，某个值等于平均值 k 个标准差的概率大于或等于 1 减去 1 除以k平方的比率。

因此，切比雪夫定理的公式如下：

金子

是随机变量的值，

变量的算术平均值，

其标准差和

要计算概率的平均值的标准偏差数。

请注意，仅当执行计算的标准差数大于 1，或者换句话说，如果k大于 1 时，才能使用此公式。

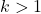您可以使用下面的在线切比雪夫定理计算器来计算概率。

切比雪夫定理的示例

一旦我们了解了切比雪夫定理的定义及其公式是什么，下面是该统计定理的一个已解决的示例，以便更好地理解该概念。

• 如果大学课程统计中的成绩按照平均值为 65、标准差为 10 的分布来定义，那么获得 50 到 80 之间成绩的学生所占的百分比是多少？

为了解决这个问题，我们需要应用切比雪夫定理的公式。然而，我们必须首先确定值 50 和 80 与变量平均值有多少标准差，为此，我们只需进行以下计算：

因此，值 50 和 80 分别对应于下均值和上均值的 1.5 个标准差。因此，我们使用 k=1.5 时切比雪娃定理的公式：

因此，至少 55.56% 的学生获得了 50 至 80 分之间的成绩。

切比雪夫定理计算器

输入相关值与平均值(k)之间的标准差数，然后单击“计算”。然后计算器将返回置信区间的最小概率。

您必须使用点作为小数点分隔符来输入标准差数。

切比雪夫定理和经验法则

统计学中两个密切相关的概念是切比雪夫定理和经验规则，因为两者都用于计算置信区间的概率。

切比雪夫定理与经验规则之间的区别在于，切比雪夫定理可以用于任何类型的分布，而经验规则仅对正态分布有效。

因此，切比雪夫定理的用途更广泛，但经验规则为正态分布提供了更精确的结果。

单击此处查看具体的经验法则是什么：