日期连续性校正：定义和示例

卡方独立性检验用于确定两个分类变量之间是否存在显着关联。

该检验使用以下原假设和备择假设：

• H ₀ ：（零假设）两个变量是独立的。
• H ₁ ：（替代假设）两个变量不是独立的。 （即它们是关联的）

我们使用以下公式计算此检验的卡方 x ²检验统计量：

X ² = Σ(O _i -E _i ) ² / E _i

金子：

• Σ：是一个奇特的符号，意思是“和”
• O：观测值
• E：期望值

该检验假设列联表中频率的离散概率可以通过卡方分布来近似，卡方分布是一种连续分布。

然而，这种假设往往有点不正确，并且所得的检验统计数据往往会向上偏差。

为了纠正这种偏差，我们可以应用Yate 的连续性校正，它将以下校正应用于公式^X2 ：

X ² = Σ(|O _i -E _i | – 0.5) ² / E _i

我们通常仅当列联表中至少一个单元格的预期频率小于 5 时才使用此校正。

示例：Yate 连续性校正的应用

假设我们想知道性别是否与对政党的偏好相关。我们对 40 名选民进行了简单的随机抽样，并询问他们的政党偏好。下表列出了调查结果：

以下是如何使用 Yate 连续性校正执行独立性的卡方检验：

观察值：

预期值：

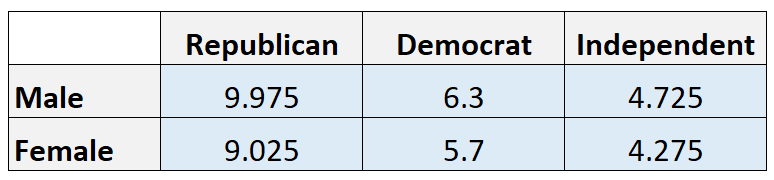
注意：我们通过将行总计乘以列总计，然后除以总计来计算每个单元格中的预期值。例如，共和党男性的预期数量为 (21*19)/40 = 9.975。

_卡^方检验_统计量：

• (|8-9.975| – 0.5) ² / 9.975 = 0.218
• (|9-6.3| – 0.5) ² / 6.3 = 0.768
• (|4-4.725| – 0.5) ² / 4.725 = 0.011
• (|11-9.025| – 0.5) ² / 9.025 = 0.241
• (|3-5.7| – 0.5) ² / 5.7 = 0.849
• (|5-4.275| – 0.5) ² / 4.275 = 0.012

^所以，

P 值：根据卡方 P 值计算器，对应于具有 2 个自由度的卡方检验统计量的 p 值为0.3501 。

由于该 p 值不小于 0.05，因此我们将无法拒绝原假设。这意味着我们没有足够的证据表明性别和政党偏好之间存在关联。