如何使用小数创建茎叶图
茎叶图是一种通过将数据集中的每个值划分为“茎”和“叶”来显示数据的图表类型。
例如，假设我们有以下数据集：
数据集： 12、14、18、22、22、23、25、25、28、45、47、48
如果我们将每个值的第一个数字定义为“茎”，第二个数字定义为“叶”，那么我们可以创建以下茎叶图：
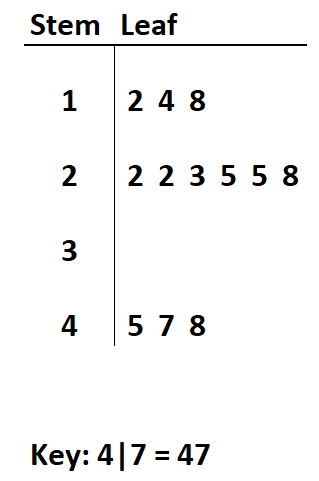
虽然茎叶图通常与整数值一起使用，但它们也可以用于带有小数位的值。
以下示例说明如何使用小数创建茎叶图。
示例 1：具有一位小数的茎叶图
假设我们有以下数据集：
数据集： 11.6、12.2、12.5、12.6、13.7、13.8、14.1、15.2
如果我们将逗号之前的数字定义为茎，将逗号之后的数字定义为叶，那么我们可以创建以下茎叶图：
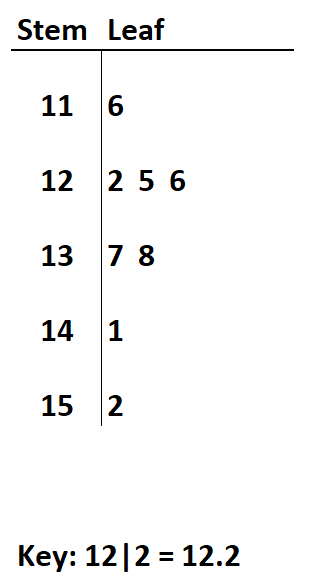
创建此茎叶图时，重要的是在底部包含一个键，以便读者知道如何解释茎叶值。
示例 2：具有多个小数位的茎叶图
假设我们有以下数据集：
数据集： 3.26、3.28、3.34、3.38、3.41、3.42、3.44、3.59、3.63
如果我们将整数和小数点后的第一个值设置为茎，将小数点后的第二个值设置为叶子，那么我们可以创建以下茎叶图：
同样，图底部的键告诉我们如何解释图值。
示例 3：用小数解释茎叶图
假设我们有以下带小数的茎叶图：
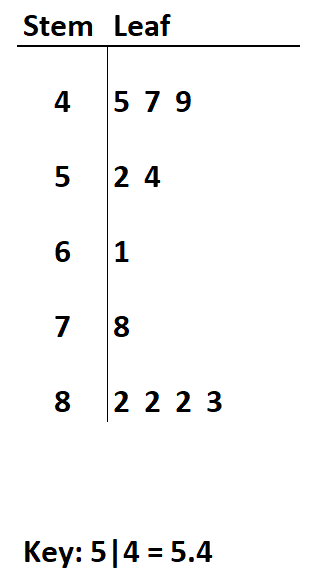
问题1：数据集中的最大值是多少？
最大值为8.3 。
问题2：数据集的范围是什么？
数据集的极差是最大值和最小值之间的差。所以范围是 8.3 – 4.5 = 3.8 。
问题3：数据集的模式是什么？
众数是最常出现的值。那将是8.2 。
问题4：数据集的中位数是多少？
中位数定义为数据集的“平均”值。为了找到这个值，我们可以将每个单独的值写入数据集中并找到中值：
数据集： 4.5、4.7、4.9、5.2、5.4、6.1、7.8、8.2、8.2、8.2、8.3
中位数是6.1 。
其他资源
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多