什么是单峰分布? (定义&;示例)
单峰分布是具有明显峰值的概率分布。
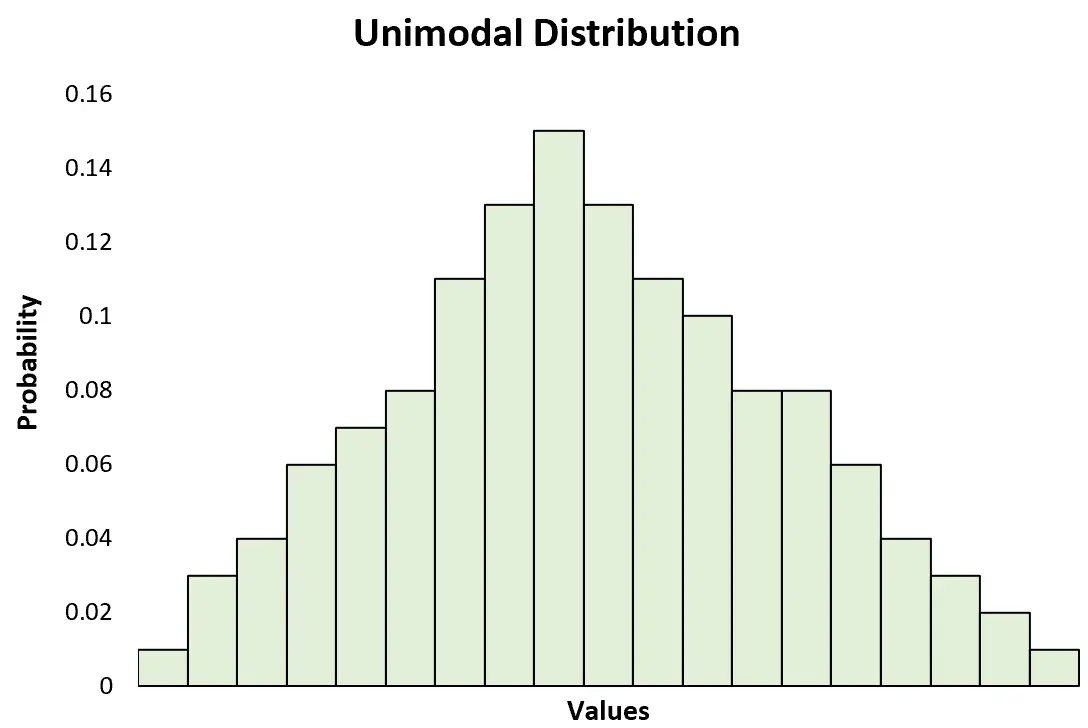
这与双峰分布形成对比,双峰分布有两个明显的峰值:
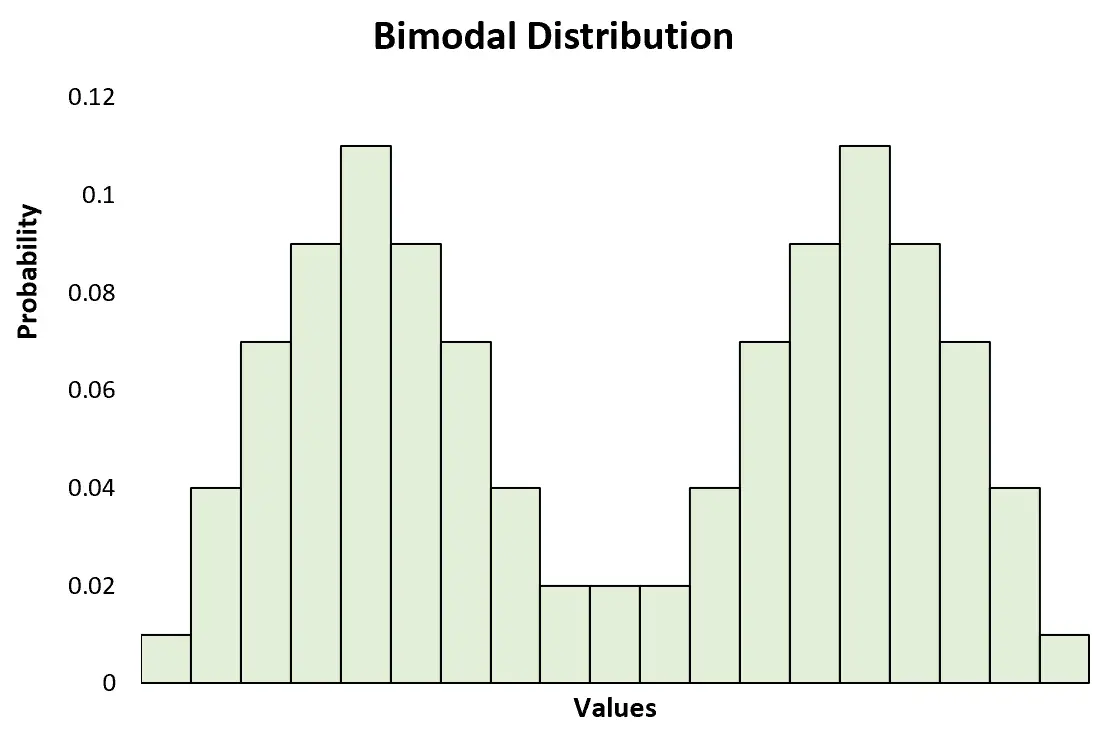
这也与具有两个或更多峰值的多峰分布形成对比:
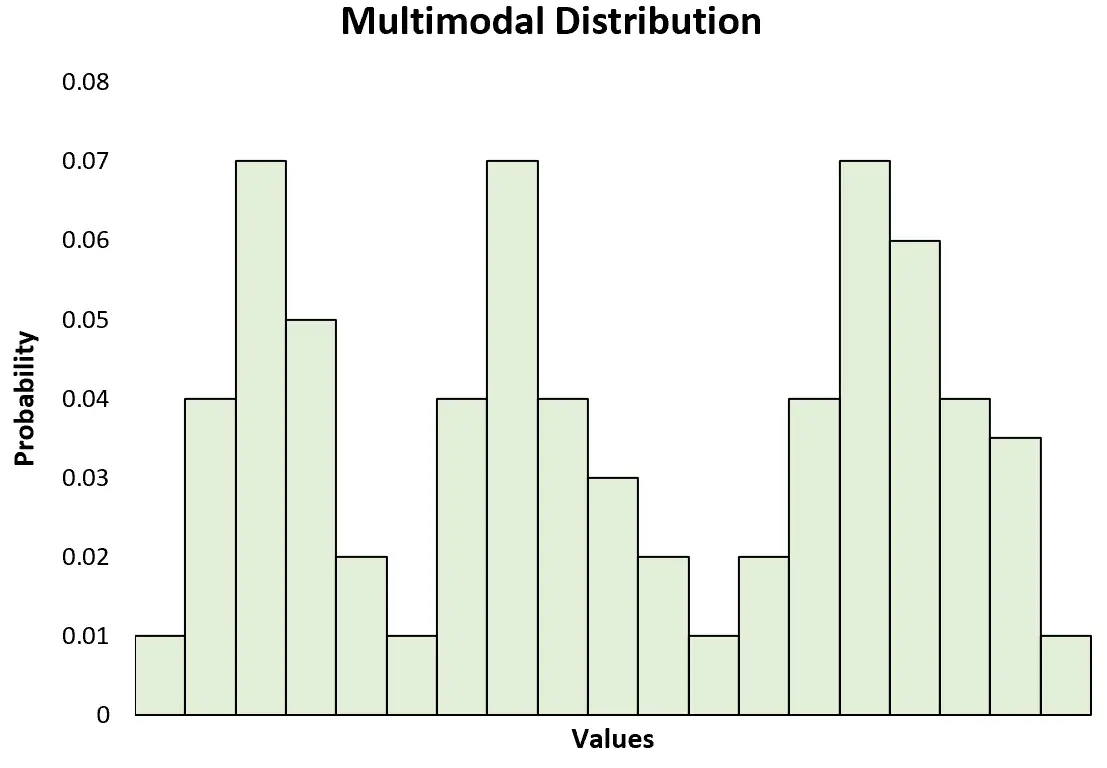
注意:双峰分布只是多峰分布的一种特定类型。
单峰分布的示例
以下是实践中单峰分布的一些示例。
示例1:婴儿的出生体重
众所周知,新生儿的体重分布遵循单峰分布,平均约为 7.5 磅。如果我们创建婴儿体重的直方图,我们会看到“峰值”为 7.5 磅,一些婴儿体重较重,另一些婴儿体重较轻。

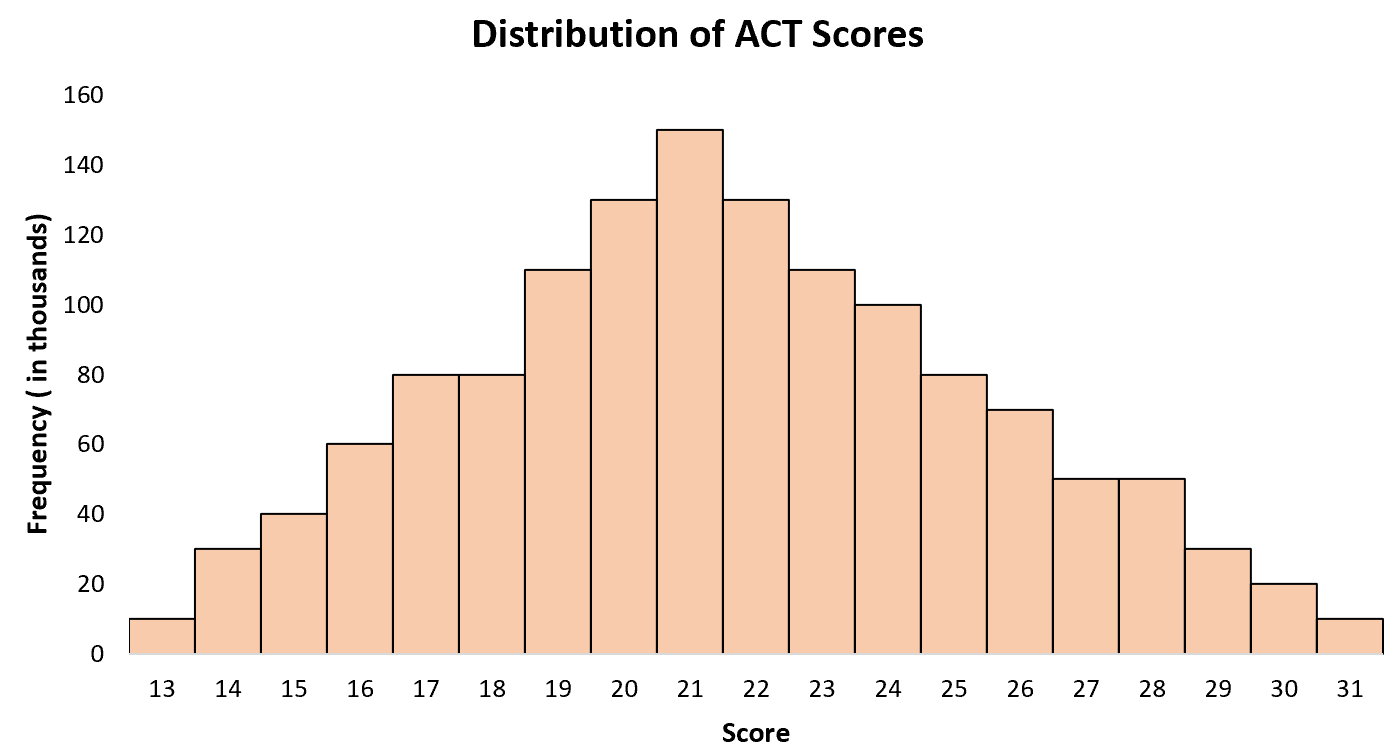
示例 2:ACT 分数
美国高中生的ACT平均分在21分左右,有的学生得分较低,有的学生得分较高。如果我们为美国所有学生创建 ACT 分数的直方图,我们将在 21 岁时看到一个“峰值”,其中一些学生的分数较高,而另一些学生的分数较低。
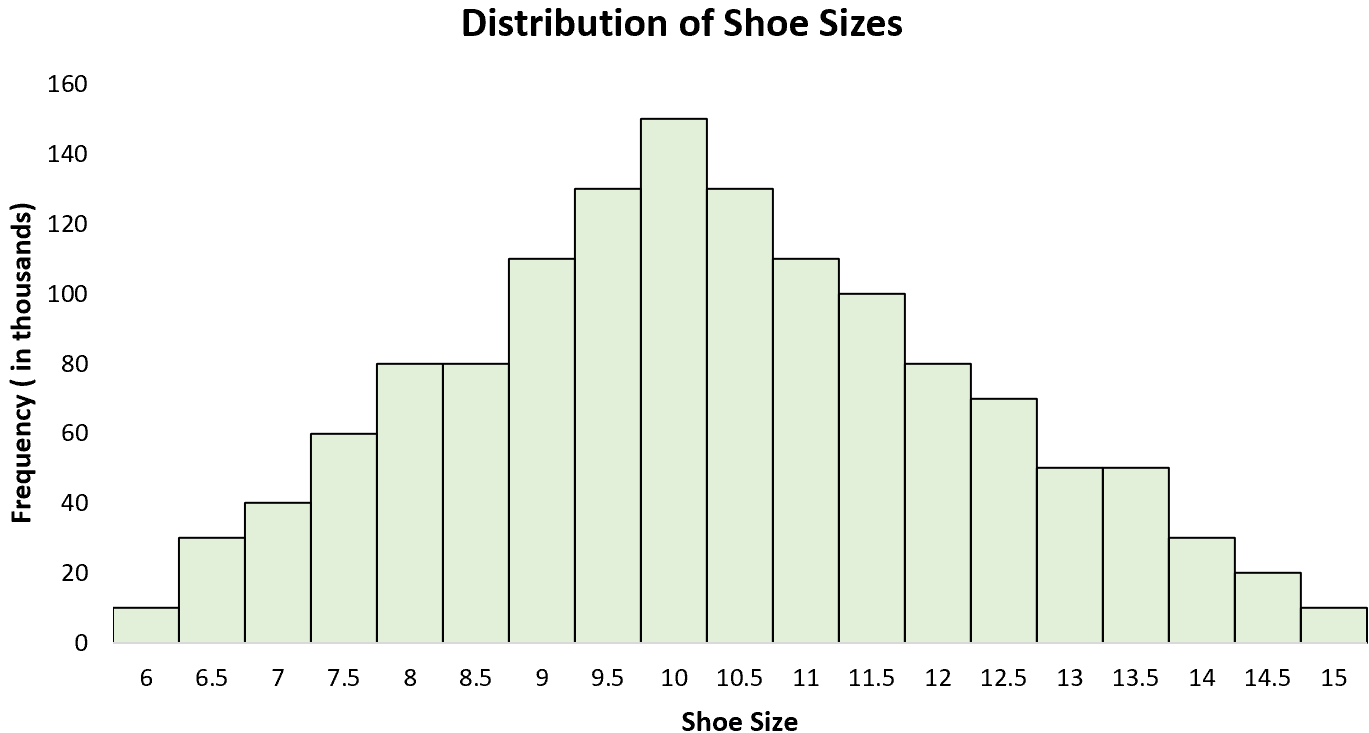
示例 3:鞋码
男士鞋码的分布是单峰分布,“峰值”在 10 左右。如果我们创建所有男士鞋码的直方图,我们将在 10 处看到一个峰值,其中一些男士穿着较大的鞋码,而其他男士则穿着较大的鞋码尺寸。尺寸较小。
统计中的单峰分布
统计中的以下概率分布都是单峰分布:
正态分布
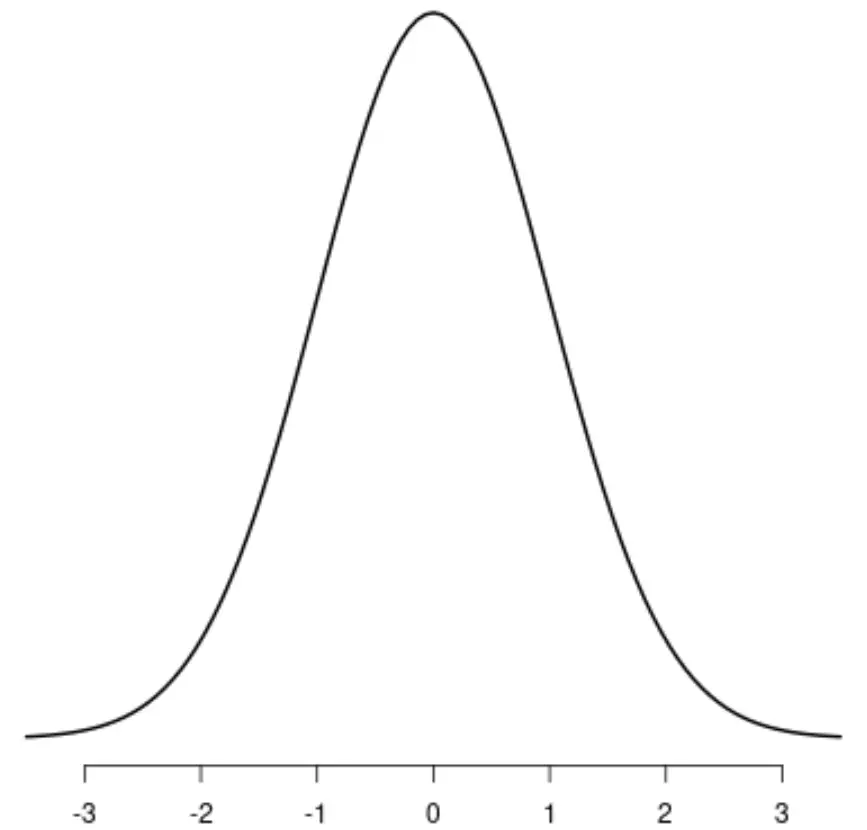
分布t
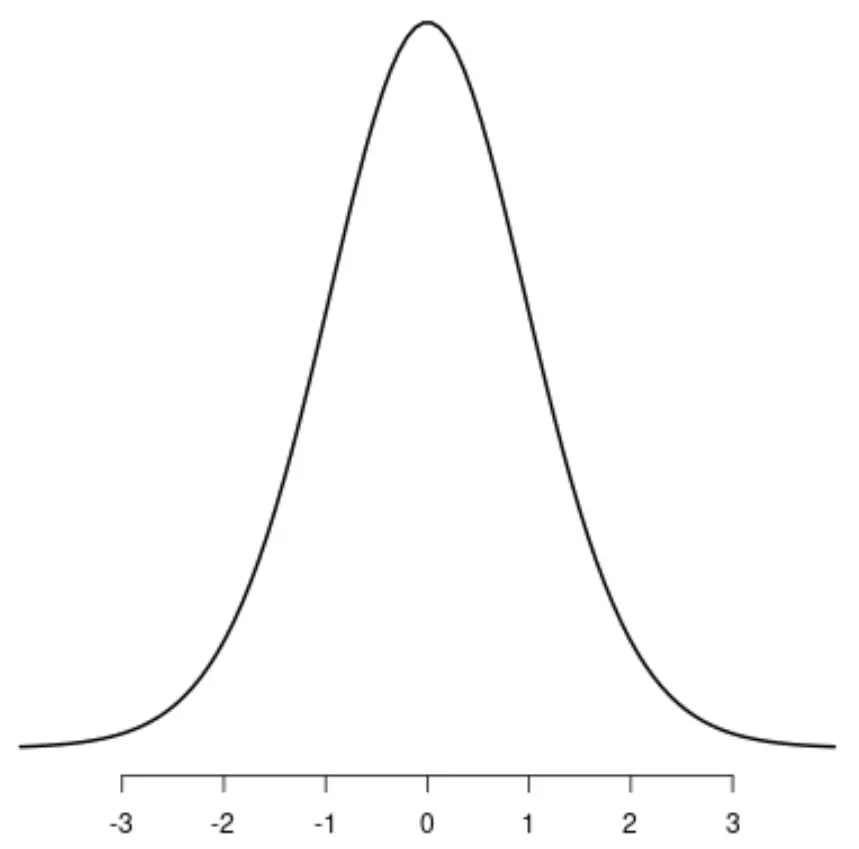
均匀分布

柯西分布
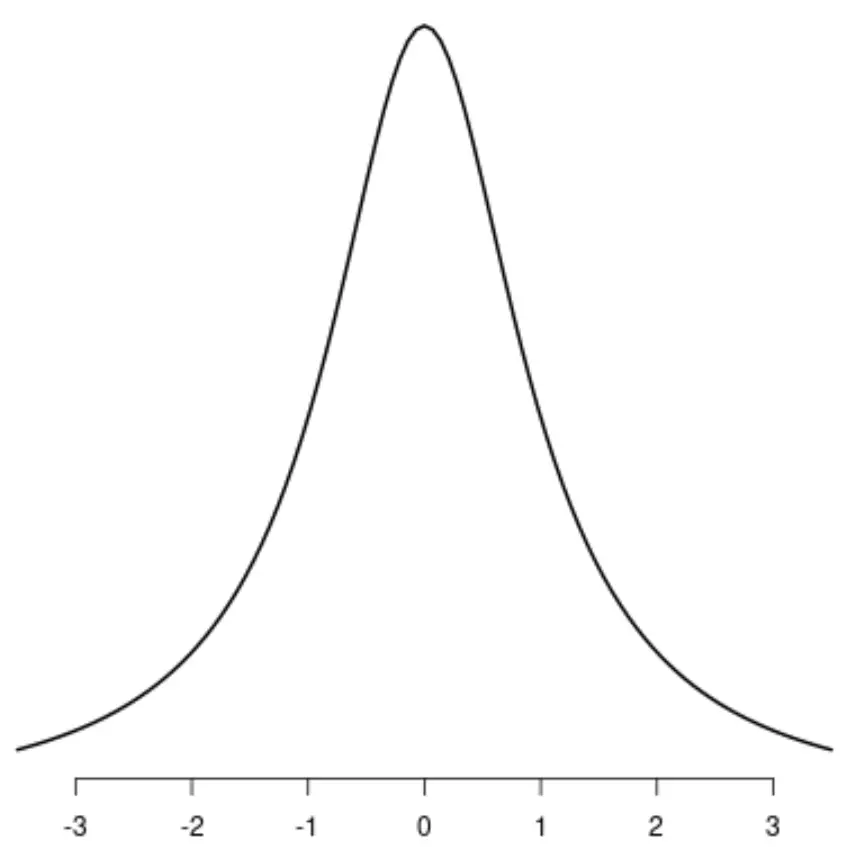
请注意,每个分布都有一个不同的峰值。
如何分析单峰分布
我们经常使用三种不同的集中趋势度量来描述单峰分布:
- 平均值:平均值
- 中位数:中值
- Mode : 最常出现的值
根据分布的不对称性,这三个测量值可以在不同的地方找到。
左偏分布:平均值 < 中位数 < 众数
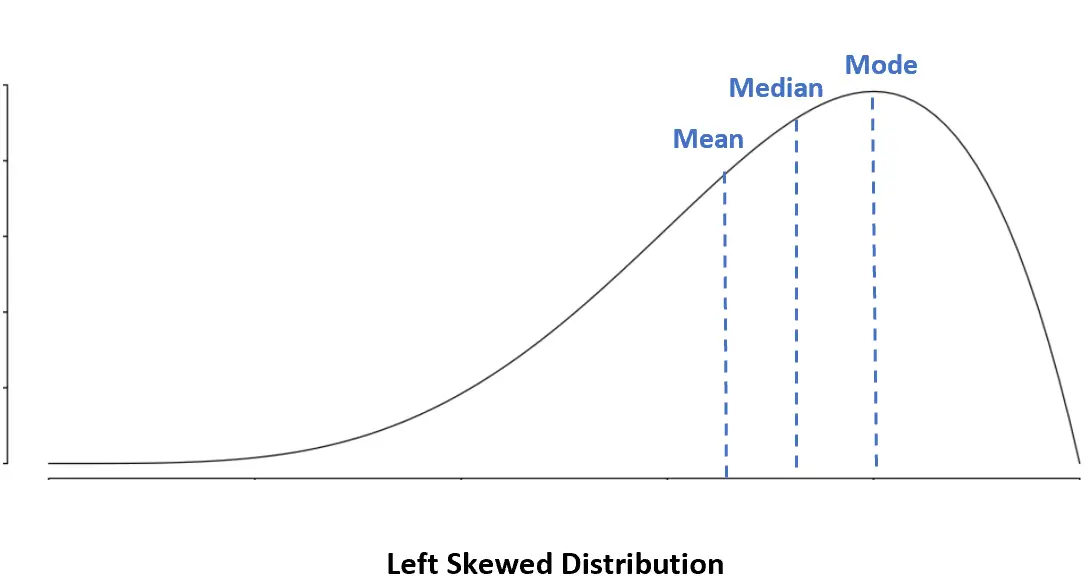
在左偏分布中,均值小于中位数。
右偏分布:众数 < 中位数 < 平均值
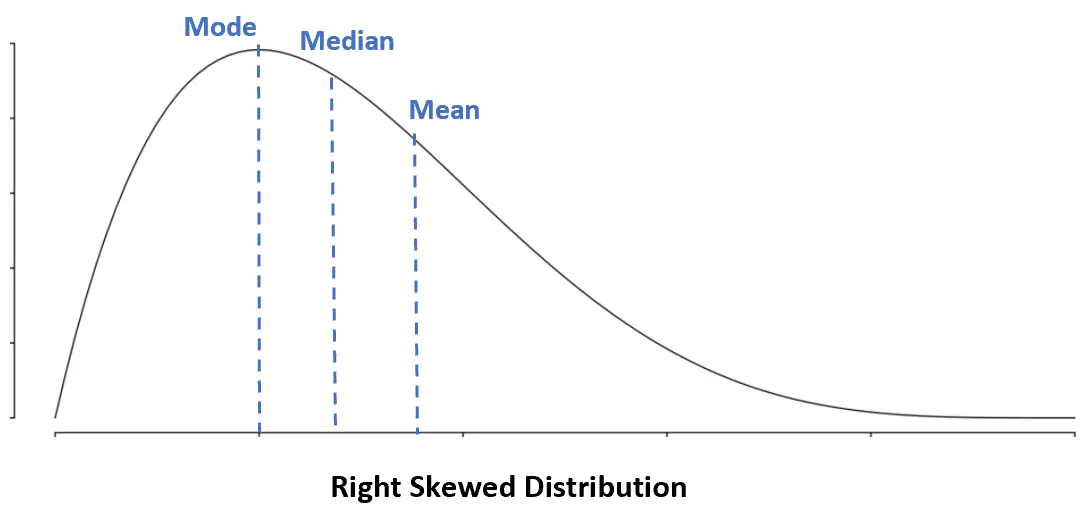
在右偏分布中,均值大于中位数。
无偏差:均值 = 中位数 = 众数

在对称分布中,均值、中位数和众数都相等。