如何在excel中计算sst、ssr和sse

我们经常使用三个不同的平方和值来衡量回归线实际拟合数据集的程度：

1. 总平方和 (SST) –各个数据点 (y _i ) 与响应变量平均值 ( y ) 之差的平方和。

• 海温 = Σ(y _i – y ) ²

2. 平方和回归 (SSR) – 预测数据点 (ŷ _i ) 与响应变量平均值 ( y ) 之间的差值的平方和。

• SSR = Σ(ŷ _i – y ) ²

3. 误差平方和 (SSE) – 预测数据点 (ŷ _i ) 与观测数据点 (y _i ) 之间差异的平方和。

• SSE = Σ(ŷ _i – y _i ) ²

以下分步示例展示了如何在 Excel 中计算给定回归模型的每个指标。

第 1 步：创建数据

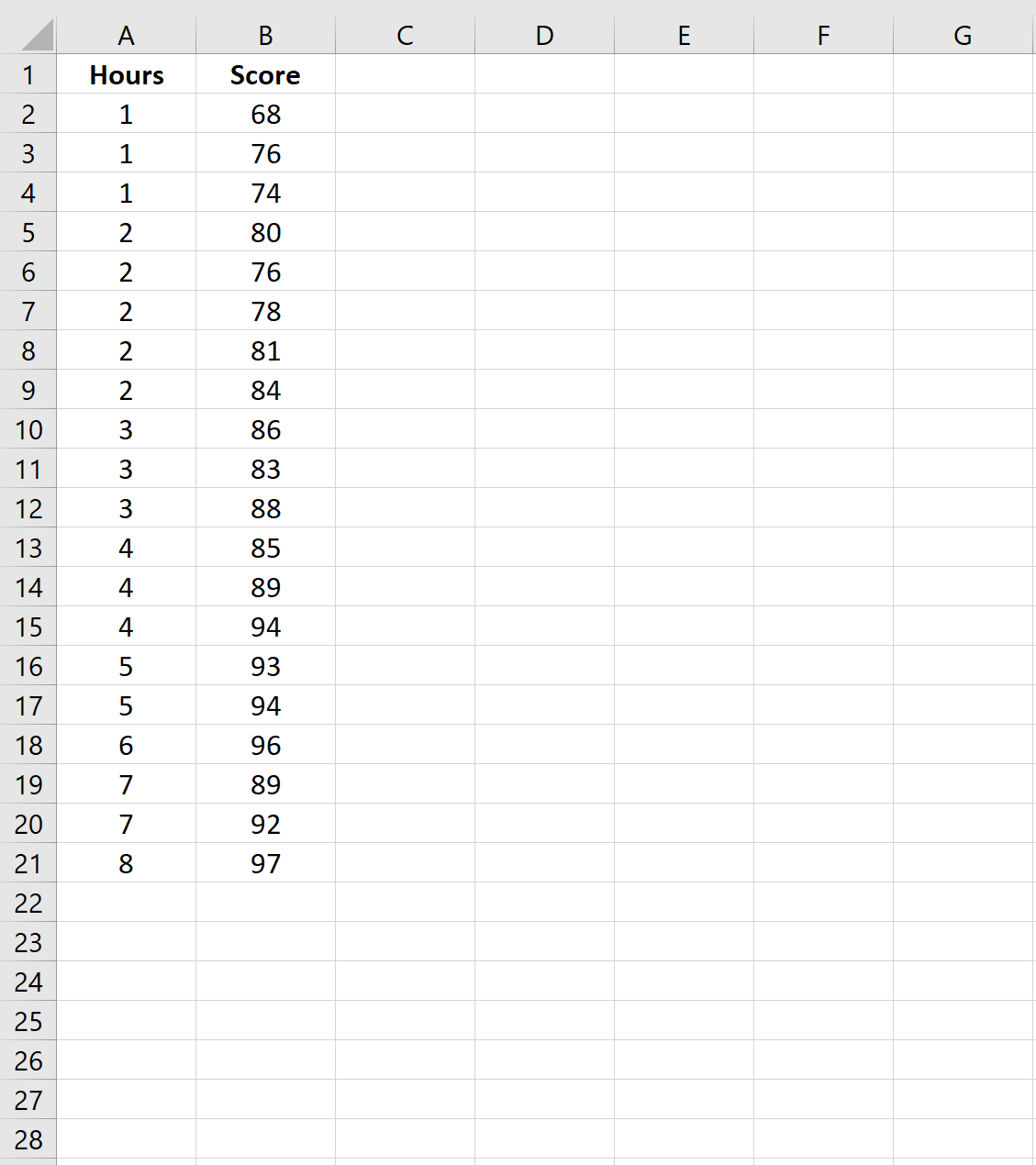
首先，我们创建一个数据集，其中包含给定学校 20 名不同学生的学习小时数和考试成绩：

第 2 步：拟合回归模型

在 Excel 的顶部功能区上，单击“数据”选项卡，然后单击“数据分析” 。如果您没有看到此选项，则必须首先安装免费的分析工具库软件。

单击“数据分析”后，将出现一个新窗口。选择回归并单击确定。

在出现的新窗口中，提供以下信息：

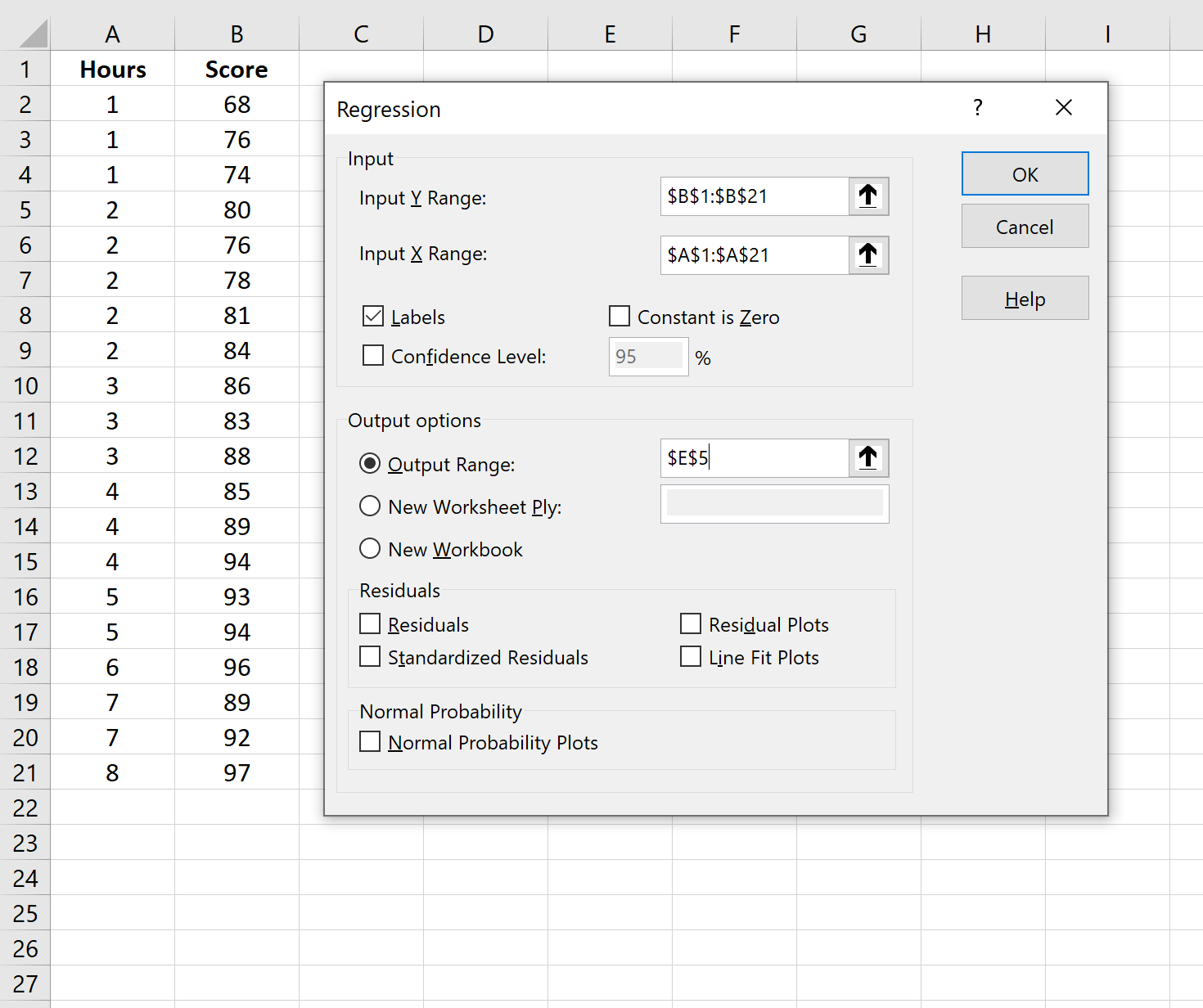
单击“确定”后，将出现回归输出。

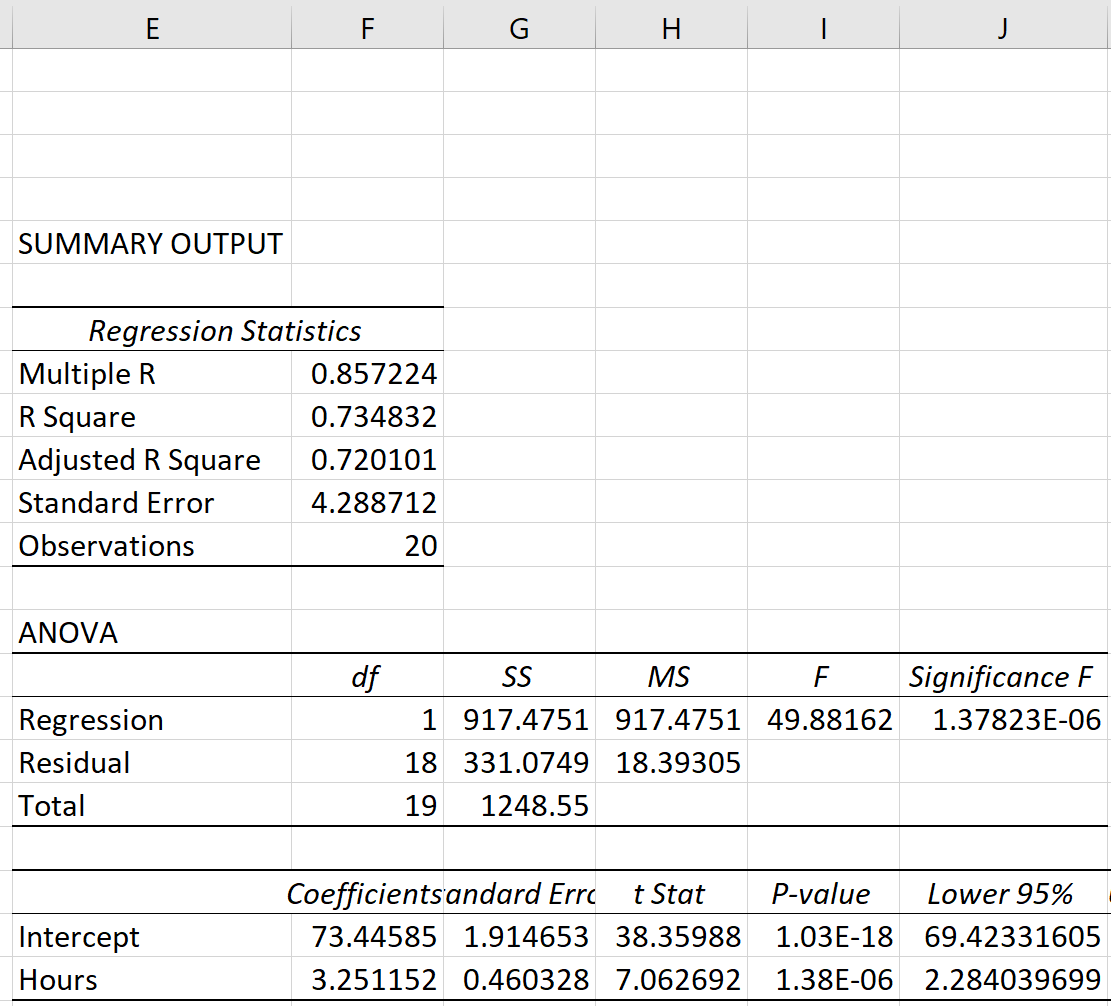
第 3 步：分析结果

三个平方和指标 – SST、SSR 和 SSE – 可以在ANOVA表的SS列中看到：

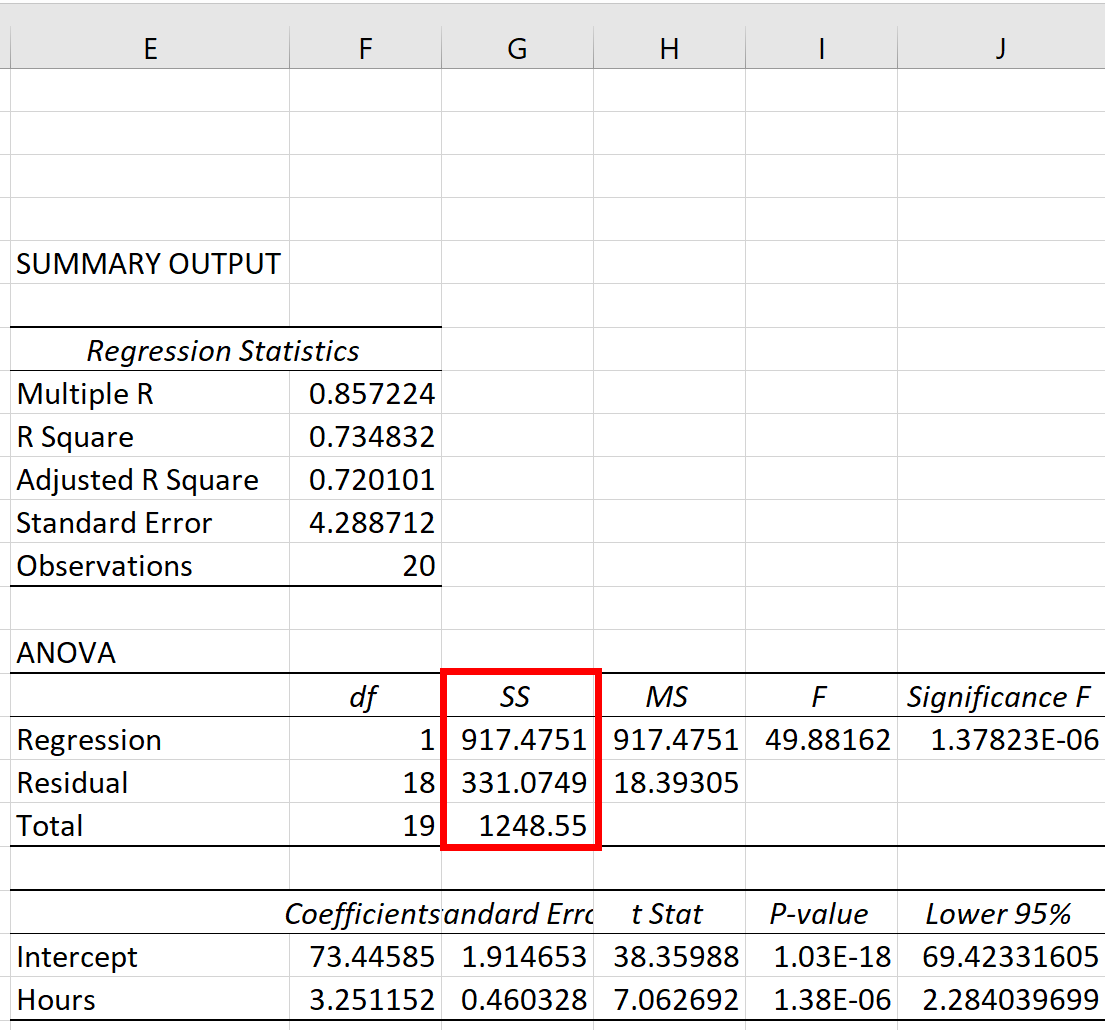
指标结果是：

• 总平方和 (SST)： 1248.55
• 平方和回归 (SSR)： 917.4751
• 误差平方和 (SSE)： 331.0749

我们可以验证 SST = SSR + SSE：

• SST = SSR + SSE
• 1248.55 = 917.4751 + 331.0749

我们还可以手动计算回归模型的R平方：

• R 平方 = SSR / SST
• R 平方 = 917.4751 / 1248.55
• R 平方 = 0.7348

这告诉我们， 73.48%的考试成绩差异可以通过学习时数来解释。

其他资源

如何在 Excel 中执行简单线性回归
如何在 Excel 中执行多元线性回归
如何在 Excel 中执行多项式回归
如何在 Excel 中执行指数回归