什么是样本空间？定义与示例

实验的样本空间是实验所有可能结果的集合。

例如，假设我们掷一次骰子。可能结果的样本空间包括：

样本空间 = 1, 2, 3, 4, 5, 6

使用该符号，我们将样本空间符号写为草书 S，并将结果写在括号中，如下所示：

S = {1, 2, 3, 4, 5, 6}

样本空间示例

以下是示例空间的一些其他示例：

示例1：绘制

假设我们抛一次硬币。如果我们让H = 硬币正面朝上， T = 硬币朝反面朝上，那么这次抛硬币的样本空间为：

S = {H, T}

示例 2：袋子里的弹珠

假设我们从包含三个弹珠的袋子中随机选择一个弹珠：红色弹珠、绿色弹珠和蓝色弹珠。如果我们让R = 红色、 G = 绿色、 B = 蓝色，则样本空间为：

S = {R，G，B}

示例 3：抛硬币和掷骰子

假设我们同时抛一枚硬币和掷骰子。如果我们让H1代表“Head”和“1”的结果，那么结果的样本空间为：

S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}

计数的基本原理

计数的基本原理是计算实验潜在结果总数的一种方法。

该原则指出，如果事件 A 有n 个不同的结果，事件 B 有m 个不同的结果，则潜在结果的总数可以计算如下：

总结果 = m * n

示例 1：抛硬币和掷骰子

例如，如果我们同时掷硬币和掷骰子，则样本空间中结果的总数可以计算如下：

总结果 =（硬币落地的 2 种方式）*（骰子落地的 6 种方式）= 12 种可能的结果。

我们在前面的示例中写下了这 12 个结果：

S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}

示例 2：计算服装组合

该原理还可用于计算样本空间中两个以上事件的总结果。

例如，假设一个随机抽屉包含 3 件不同的衬衫、4 条不同的裤子和 2 种不同的袜子。如果我们不看就随机选择一件衣服，则可能的服装总数将计算如下：

服装总数 = 3 * 4 * 2 = 24 种可能的服装

使用树形图可视化样本空间

当样本空间中的结果数量很大时，构建树形图来可视化结果的不同组合可能很有用。

例如，假设衣柜里有 2 件不同的衬衫、2 条不同的裤子和 2 件不同的袜子。如果我们在不看的情况下随机选择一件衣服，则可能的服装总数可以如下所示：

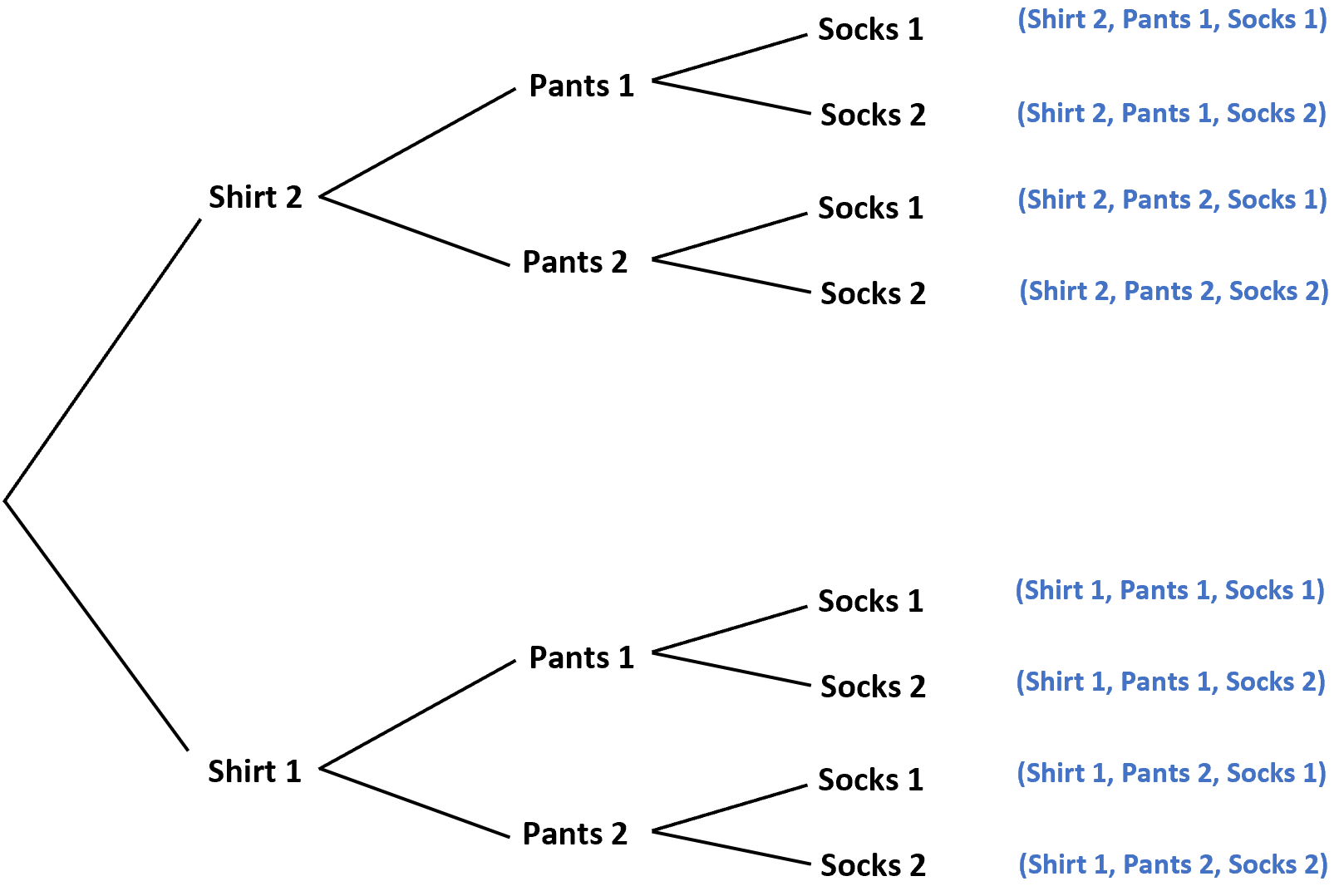
该图帮助我们可视化样本空间中八种不同的潜在结果。

我们还可以利用计数的基本原理来确认一定有八种不同的结果：

总结果 = 2 件衬衫 * 2 件裤子 * 2 件袜子 = 8 种可能的服装

计算样本空间中的结果概率

一旦我们确定了实验的样本空间，我们就可以使用以下公式计算事件A发生的概率：

P(A) =（A 的样本空间）/（总样本空间）

例如，假设我们掷一次骰子。样本空间可以写成以下形式：

S = {1, 2, 3, 4, 5, 6}

如果我们将事件A定义为骰子落在数字“2”上，那么事件A的样本空间可以写成如下：

S = {2}

因此，事件A发生的概率可以计算如下：

P(A) = 1/6

如果我们将事件A定义为骰子落在偶数上，那么事件A的样本空间可以写成如下：

S = {2, 4, 6}

因此，事件A发生的概率可以计算如下：

P(A) = 3/6