加权平均

经过本杰明·安德森博 8月 6, 2023 统计数据 0 条评论

这里我们解释什么是加权平均值以及它是如何计算的。您将能够看到关于我们如何找到加权平均值的已解决练习。而且，更重要的是，您可以使用最后的计算器计算任何数据集的加权平均值。

加权平均值是多少？

加权平均值是描述性统计中心性的度量。计算加权平均值时，必须首先将每个统计数据乘以其权重（或权重），然后将所有乘积相加，最后将加权总和除以所有权重之和。

换句话说，加权平均的公式如下：

其中 x _i代表每个数据样本，w _i代表相应的权重。

因此，一条数据的权重越大，在加权平均值的计算中就越重要。也就是说，某条数据的权重越高，对加权平均的结果影响就越大。

加权平均值对于计算成绩特别有用，因为它允许您以不同的重要性评估课程期间进行的练习或考试。加权平均数还用于计算CPI（消费者价格指数），这是衡量人口价格的指标。

除加权平均外，还有几何平均、算术平均、平方平均、调和平均等其他类型的平均。

如何计算加权平均值

要计算加权平均值，必须遵循以下步骤：

将每个统计数据乘以相应的权重。
将上一步中计算出的所有乘积相加。
将上面的加权总和除以所有权重的总和。
所得结果为统计样本的加权平均值。

👉您可以使用下面的计算器来计算任何数据集的加权平均值。

加权平均示例

考虑到加权平均值的定义，我们现在将解决一个练习，以充分理解如何从一组数据获得加权平均值。

一名高中一年级学生在数学科目中获得以下成绩：部分考试 7 分（占 30%）、小组作业 9 分（占 20%）、课堂练习（带权重）6 分期末考试得分为 10%，期末考试得分为 8 分，权重为 40%。您该科目的最终成绩是多少？

要确定学生的分数，您必须使用陈述给出的值找到加权平均值。为此，我们应用加权平均公式：

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

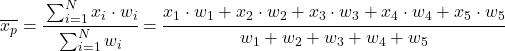
每个交付成果的得分是统计值，其百分比对应于该值的权重。因此，我们将数值和权重代入公式中，进行加权平均计算：

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

因此，该学生的最终数学成绩将为 7.7，因为这是根据加权平均值获得的结果。

加权平均计算器

将任何统计样本的数据及其各自的权重输入下面的计算器以计算其加权平均值。

在第一个框中输入统计数据，在第二个框中输入各自的权重。您必须按照与数据相同的顺序并以十进制格式写入权重。所有数字必须用空格分隔，并使用句点作为小数点分隔符输入。

标准化重量

正如我们所看到的，在加权平均值中，权重是赋予每条数据以赋予其或多或少重要性的值。因此，如果信息非常重要，它的权重就会非常高，但如果信息相关性不是很高，它的权重就会非常低。

归一化权重是一种加权方法，用于无需进行任何除法即可获得加权平均值。

归一化权重是数据项的权重除以所有权重的总和。

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

因此，所有归一化权重的总和等于 1：

$\sum_{i=1}^N w_i'=1$

因此，要使用归一化权重计算加权平均值，只需将每个数据项乘以其归一化权重即可：

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

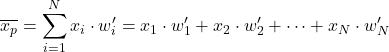
例如，我们有一个统计样本，其数据为 24, 35, 17, 41，其权重分别为 4, 9, 6, 3。为了求出该数据集的加权平均值，我们可以首先通过除以计算归一化权重每个权重除以所有权重之和：

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

现在只需将每个数据乘以其归一化权重，结果就是加权平均值：

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

加权平均与算术平均的区别

加权平均和算术平均的计算以相同的方式完成，因为必须执行类似的操作。在加权平均中，每个数据点乘以其权重并除以权重之和，但在算术平均中，将所有数据加在一起并除以数据点总数。

加权平均和算术平均的区别在于其概念，因为算术平均认为所有数据具有相同的值，而加权平均中每个数据具有不同的权重。

请注意，如果所有权重相等，则加权平均值相当于算术平均值。您可以看到下面的数学证明：

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

关于作者

本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多