布雷-柯蒂斯相异性：定义和示例

布雷-柯蒂斯相异性以J. Roger Bray和John Thomas Curtis的名字命名，是一种测量两个不同站点之间相异性的方法。

它经常用于生态学和生物学中，以量化两个地点之间发现的物种之间的差异。

Bray-Curtis 相异度计算如下：

BC _ij = 1 – (2*C _ij ) / (S _i + S _j )

金子：

• C _ij ：每个地点发现的物种最低值的总和。
• _Si :在第 i 个地点计数的样本总数
• S _j ：在j点计数的样本总数

Bray-Curtis 相异度始终介于 0 和 1 之间，其中：

• 0表示两个站点没有差异。换句话说，它们每种物种的数量完全相同。
• 1表示两个站点完全不同。换句话说，它们不共享任何同一类型的物种。

以下示例显示如何计算两个站点的 Bray-Curtis 相异度。

示例：Bray-Curtis 相异度的计算

假设一位植物学家出去统计两个不同地点的五种不同植物物种（A、B、C、D 和 E）的数量。

下表总结了她收集的数据：

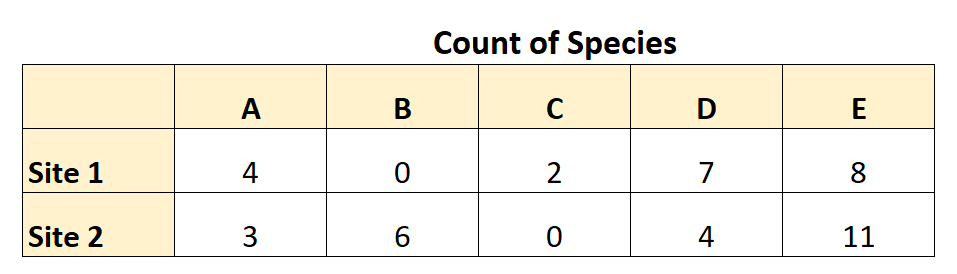
使用这些数据，她可以计算 Bray-Curtis 相异度，如下所示：

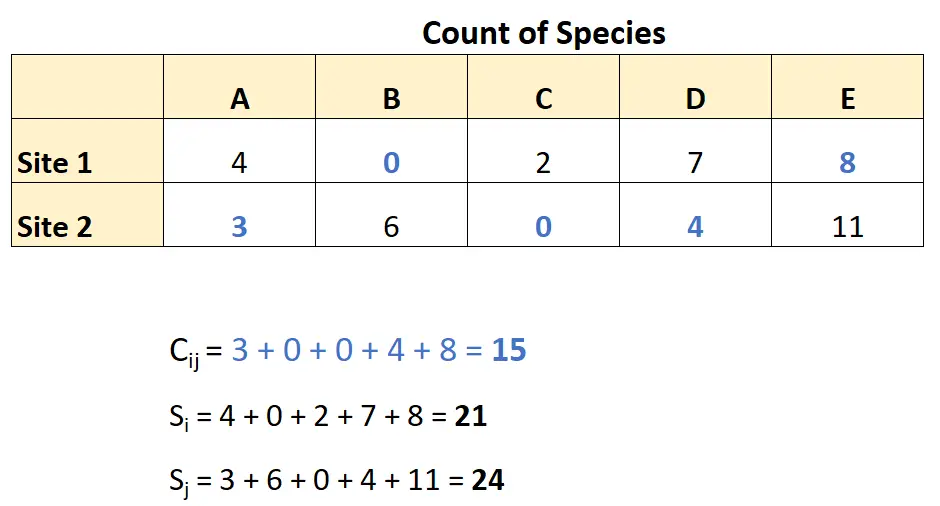
通过将这些数字积分到 Bray-Curtis 相异度公式中，我们得到：

• BC _ij = 1 – (2*C _ij ) / (S _i + S _j )
• BC _ij = 1 – (2*15) / (21 + 24)
• _BCij = 0.33

这两个位点之间的 Bray-Curtis 差异为0.33 。

Bray-Curtis 相异性的关键假设

布雷-柯蒂斯相异性假设两个站点大小相等。

这是一个至关重要的假设，因为如果一个地点比另一个地点大四倍，那么大地点自然会比小地点拥有更多的物种，仅仅是因为需要覆盖的面积要大得多。

为了说明这一点，假设植物学家收集数据的一个站点比另一个站点大四倍：

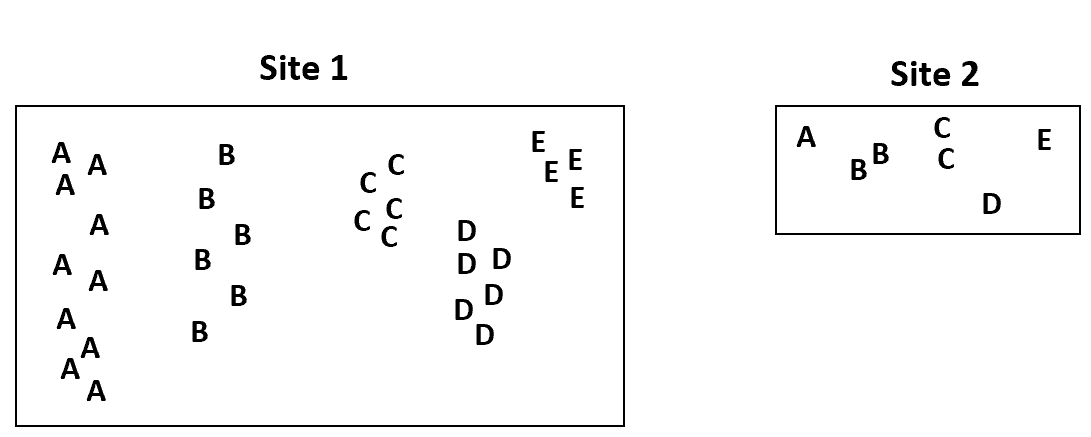
我们预计站点 1 的物种出现频率要高得多，因为它比站点 2 大得多。

所以当我们计算Bray-Curtis相异时，它会非常大。然而，这可能会产生误导，因为两个站点之间的差异不在于其组成，而在于其大小。