伯克森偏差:定义 + 示例
伯克森偏差是研究中出现的一种偏差,当两个变量在样本数据中似乎呈负相关,但实际上在总体总体中呈正相关时。
例如,假设汤姆想要研究当地餐馆的汉堡包和奶昔质量之间的相关性。
它收集了七家不同餐厅的以下数据:
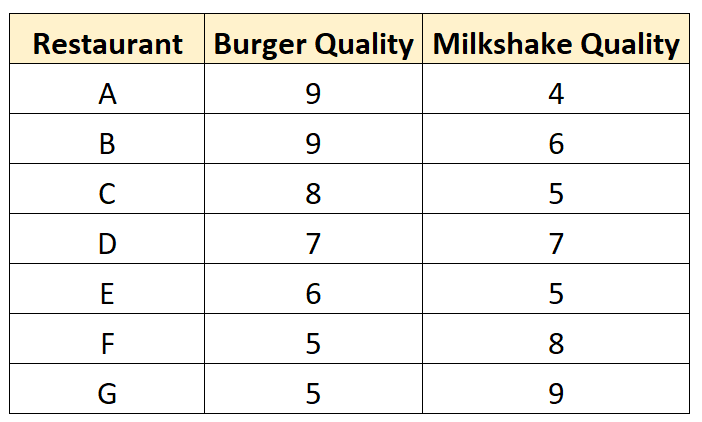
它创建一个散点图来可视化数据:
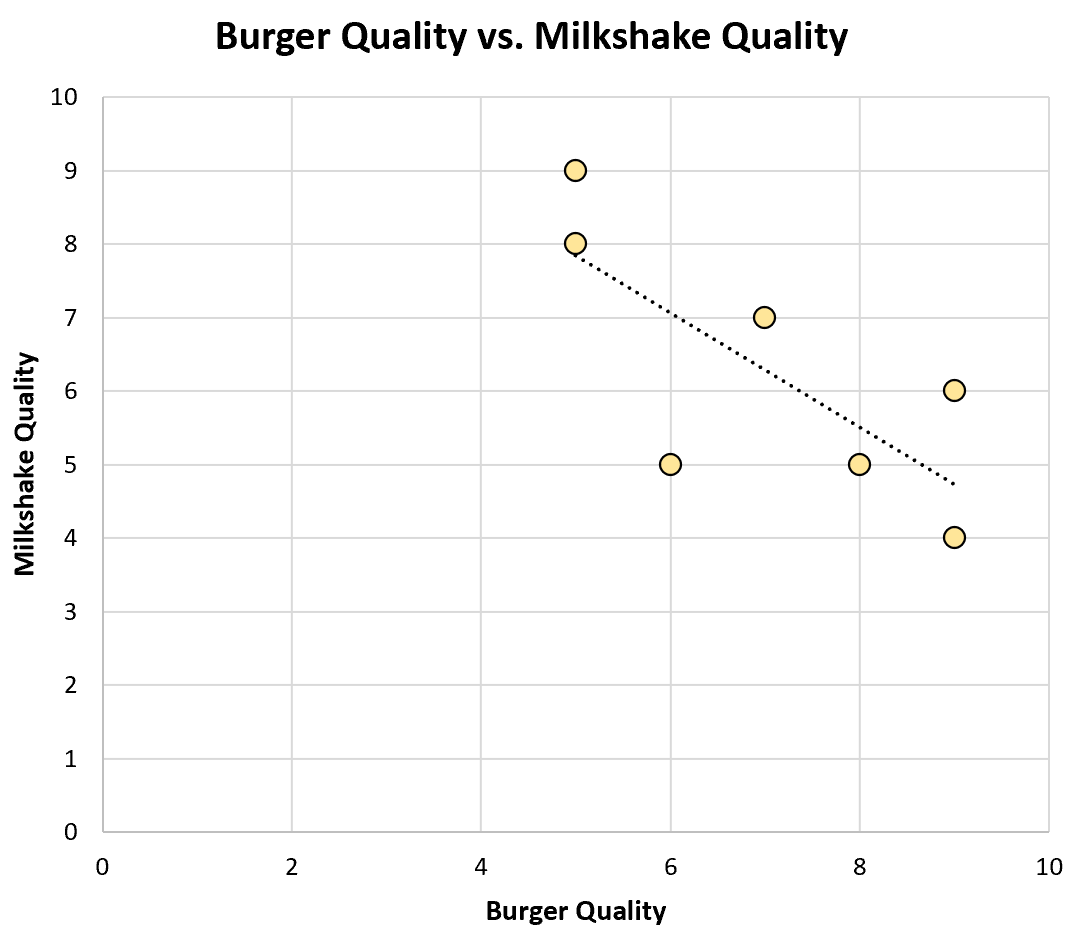
这两个变量之间的Pearson 相关系数为-0.75 ,对应于强负相关。
这一发现对汤姆来说是违反直觉的:他会认为制作美味汉堡包的餐馆也会制作美味的奶昔。
然而,事实证明,汤姆根本就忽略了镇上所有制作不好的汉堡和不好的奶昔的餐馆。
如果他去过这些餐馆,他会收集以下数据集:
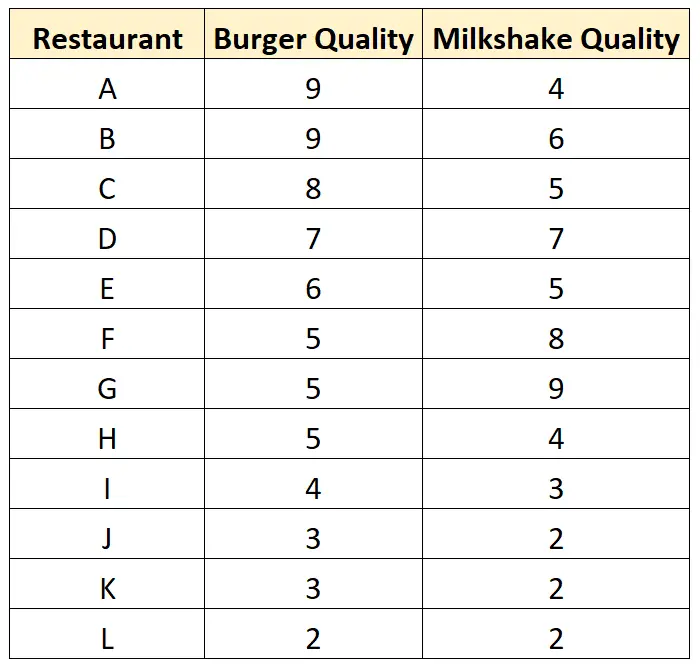
这就是该数据集的散点图的样子:
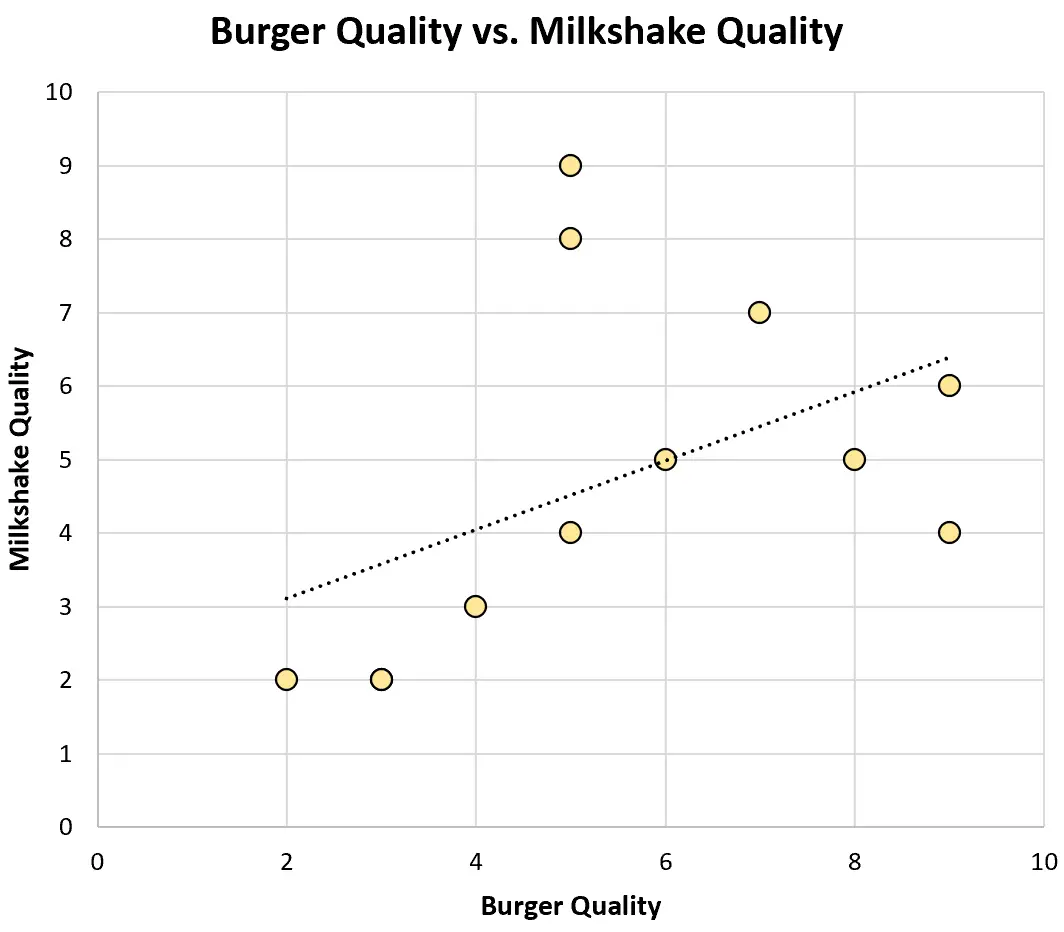
两个变量之间的Pearson 相关系数为0.46 ,呈现中等强度的正相关。
通过仅检查该市的一小部分餐厅,汤姆错误地得出结论:汉堡和奶昔的质量之间存在负相关关系。
事实上,事实证明这两个变量之间存在正相关关系(正如人们所期望的那样)。这是伯克森偏见的典型例子。
有关实践中出现 Berkson 偏差的其他场景,请参阅以下示例。
示例1:大学招生
假设一所大学只招收 GPA 和 ACT 分数足够高的学生。
众所周知,这两个变量是正相关的,但事实证明,在决定去某所大学的学生中,两者之间似乎存在负相关。
然而,这种负相关的发生只是因为 GPA 和 ACT 分数都高的学生能够进入精英大学,而 GPA 和 ACT 分数都低的学生根本不会被录取。
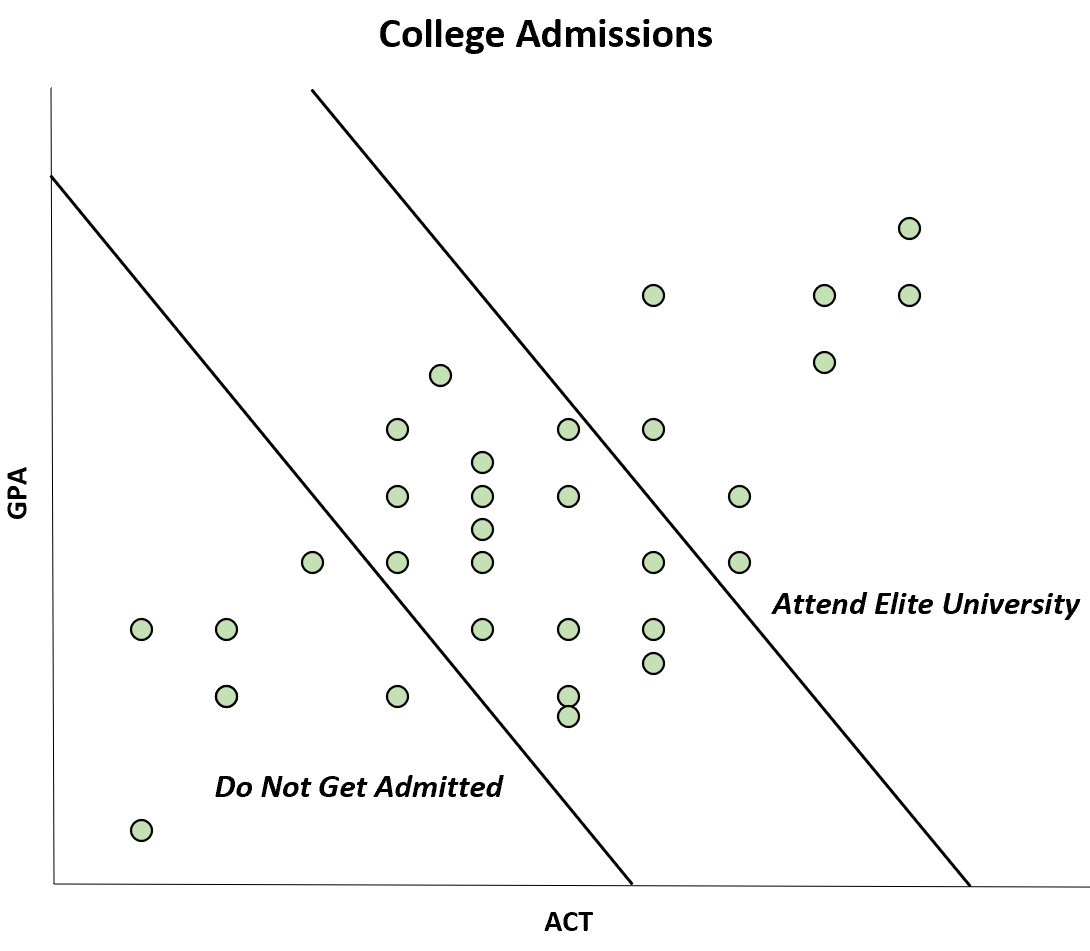
尽管 ACT 和 GPA 之间的相关性在总体中呈正相关,但在样本中却呈负相关。这是伯克森的偏见案例。
示例 2:约会偏好
许多人只会与既有吸引力又性格好的伴侣约会。
在现实世界中,这两个变量之间可能没有相关性,但是当缩小约会范围时,一个人可能会完全忽略那些既没有吸引力又很有天赋的潜在伴侣。 ‘性格很好。
因此,在潜在的伴侣中,这两个变量之间可能存在负相关关系:更具吸引力的人性格较差,而性格较好的人似乎不太有吸引力。
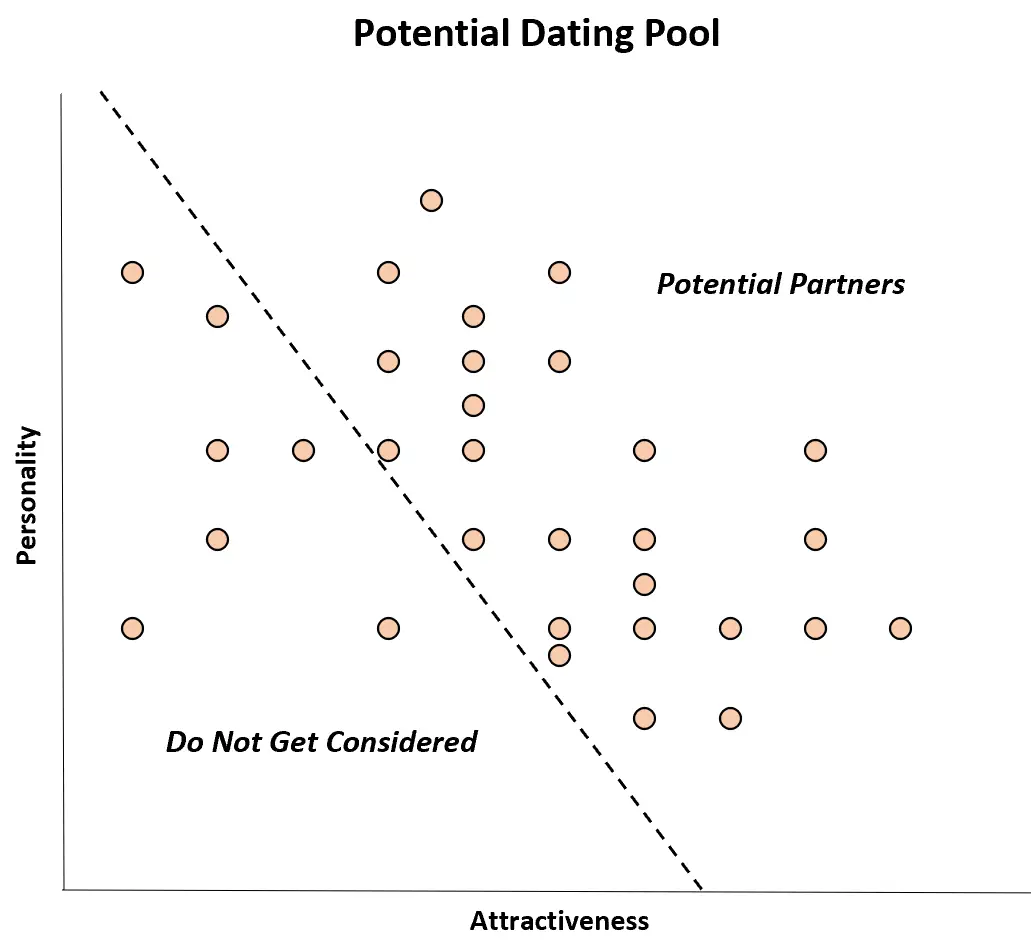
尽管这两个变量在总体中不存在相关性,但在潜在伴侣的样本中似乎存在负相关性。这只是伯克森偏见的一个例子。
如何防止伯克森偏见
在研究中避免伯克森偏差的最明显方法是从总体中收集简单的随机样本。换句话说,确保感兴趣群体的每个成员都有平等的机会被纳入样本中。
例如,如果您正在研究某个国家/地区的疾病流行情况,则需要收集来自全国各地的个人样本,而不仅仅是那些在医院中容易接触到的人。
通过使用简单的随机样本,研究人员可以最大限度地提高样本代表总体的机会,这意味着他们可以自信地将样本的发现推广到总体。