统计学中有影响力的观察是什么？

在统计学中，有影响力的观察是数据集中的观察，当删除该观察时，会显着改变回归模型的系数估计。

衡量观测影响的最常见方法是使用库克距离，它量化了当第 i^个观测被移除时，回归模型中所有拟合值发生了多少变化。

一般来说，任何库克距离大于 1 的观测值都被视为高杠杆观测值。

以下示例演示如何计算和解释给定数据集的库克距离，以检测潜在的有影响力的观测值。

示例：检测有影响的观察结果

假设我们有以下包含 14 个值的数据集：

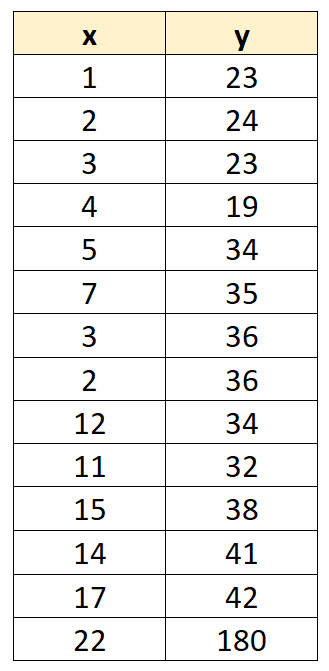
现在假设我们拟合一个简单的线性回归模型。回归结果如下所示：

使用统计软件，我们可以计算每次观测的库克距离的以下值：

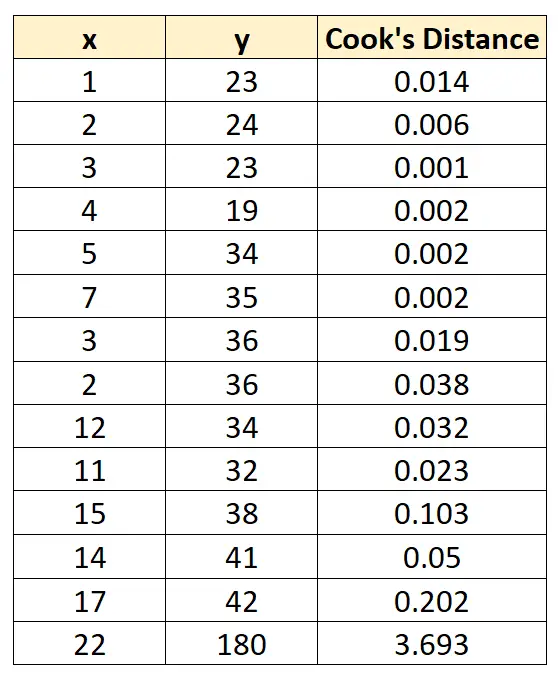
请注意，最后一个观测值的库克距离显着大于 1，这告诉我们这是一个有影响力的观测。

假设我们从数据集中删除该值并拟合一个新的简单线性回归模型。该模型的输出如下所示：

请注意，截距和 x 的回归系数都发生了巨大变化。这告诉我们，从数据集中删除有影响的观察结果完全改变了拟合的回归模型。

下图显示了这两个拟合回归方程之间的差异：

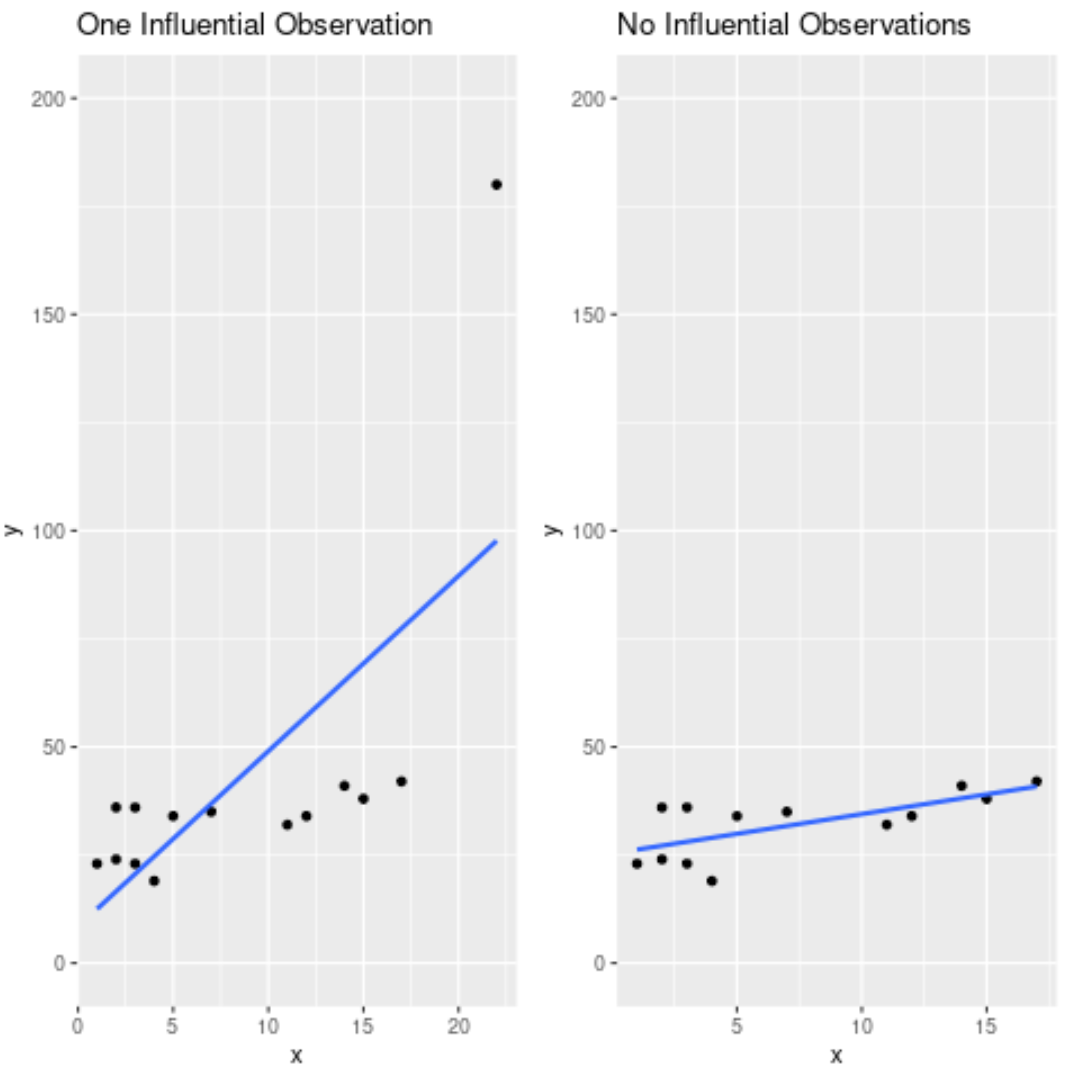
注意单个有影响的观察对回归线的改变有多大。通过删除这一观察结果，我们能够找到一条更接近数据的回归线。

评论

值得注意的是，库克距离应用于识别潜在影响的观测结果。然而，仅仅因为观察有影响并不一定意味着它应该从数据集中删除。

首先，您需要验证观察结果不是数据输入错误或其他奇怪事件的结果。如果结果证明它是合法值，那么您可以决定通过以下方式之一处理它：

• 将其从数据集中删除。
• 将其保留在数据集中。
• 将其替换为平均值或中位数等替代值。

根据您的具体情况，其中一个选项可能比其他选项更有意义。

实际中如何计算厨师距离

以下教程解释了如何使用 Python 和 R 计算给定数据集的库克距离：

如何用 Python 计算库克距离
如何计算R中的库克距离