如何在 ti-84 计算器上执行对数回归

对数回归是一种回归类型，用于对增长或下降首先快速加速然后随着时间的推移减慢的情况进行建模。

例如，下图显示了对数衰减的示例：

对于这种类型的情况，可以使用对数回归很好地对预测变量和响应变量之间的关系进行建模。

对数回归模型的方程采用以下形式：

y = a + b*ln(x)

金子：

• y：响应变量
• x：预测变量
• a、b：描述x和y之间关系的回归系数

以下分步示例展示了如何在 TI-84 计算器上对以下数据集执行对数回归：

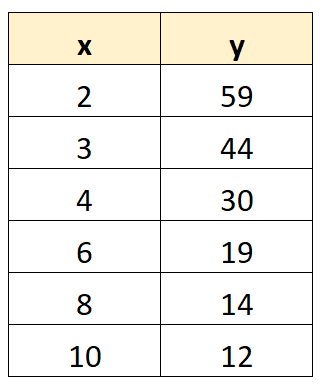
第 1 步：输入数据

首先，我们将输入数据值。按STAT ，然后按EDIT 。然后在L1列中输入数据集的x值，在L2列中输入y值：

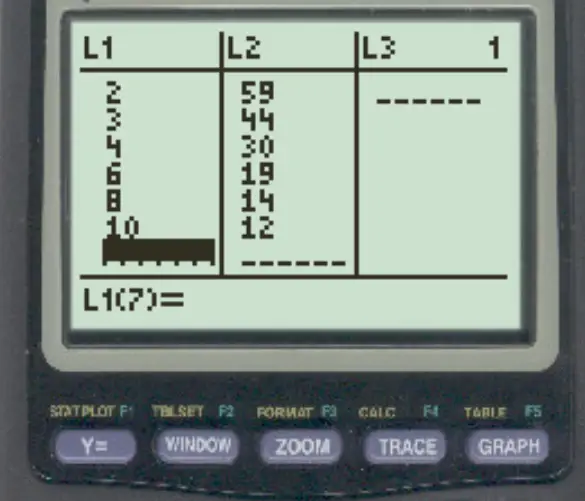
步骤 2：拟合对数回归模型

接下来，我们填写对数回归模型。

点击统计，然后滚动至计算。然后滚动至LnReg并按ENTER两次。

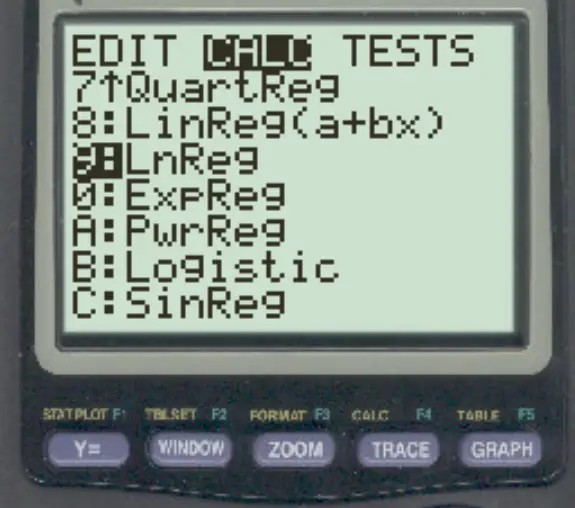
将显示以下结果：

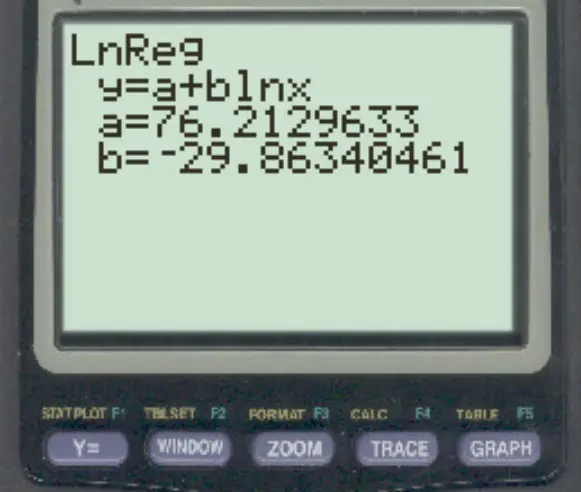
第 3 步：解释结果

我们可以使用结果中的系数编写以下调整后的对数回归方程：

y = 76.21296 – 29.8634 * ln(x)

我们可以使用该方程根据预测变量x的值来预测响应变量y 。例如，如果x = 8，那么我们预测y将为14.11 ：

y = 76.21296 – 29.8634 * ln(8) = 14.11

奖励：随意使用此在线对数回归计算器来自动计算给定预测变量和响应变量的对数回归方程。

其他资源

如何在 TI-84 计算器上执行线性回归
如何在 TI-84 计算器上执行二次回归
如何在 TI-84 计算器上执行指数回归
如何在 TI-84 计算器上创建残差图