如何解释均方根误差 (rmse)

回归分析是一种可以用来理解一个或多个预测变量与响应变量之间关系的技术。

评估回归模型对数据集的拟合程度的一种方法是计算均方误差，它是一个指标，告诉我们模型的预测值与数据集的实际值之间的平均距离。

RMSE 越低，给定模型就越能“拟合”数据集。

求均方误差的公式（通常缩写为RMSE ）为：

RMSE = √ Σ(P _i – O _i ) ² / n

金子：

• Σ 是一个奇特的符号，意思是“和”
• P _i是数据集中^{第 i 个}观测值的预测值
• O _i是数据集中^{第 i 个}观测值的观测值
• n 是样本量

以下示例显示如何解释给定回归模型的 RMSE。

示例：如何解释回归模型的 RMSE

假设我们想要建立一个回归模型，使用“学习时间”来预测学生在特定高考中的“考试成绩”。

我们收集了 15 名学生的以下数据：

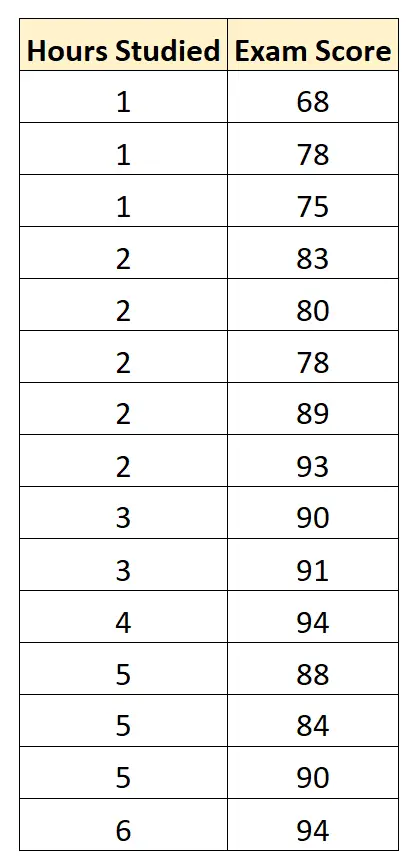
然后我们使用统计软件（如Excel、SPSS、R、Python）等。找到以下拟合回归模型：

考试成绩 = 75.95 + 3.08*（学习时间）

然后，我们可以使用这个方程根据每个学生的学习小时数来预测他们的考试成绩：

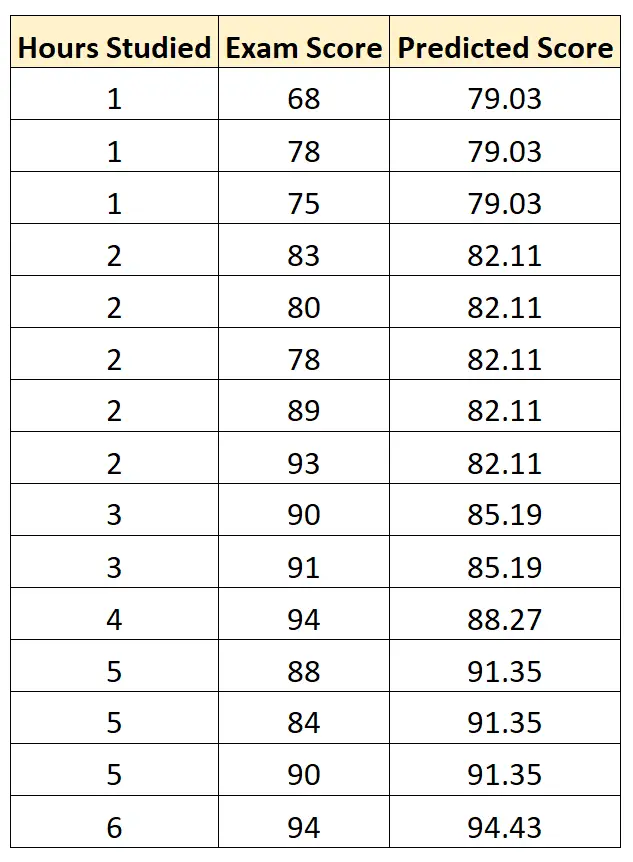
然后我们可以计算每个预测考试分数与实际考试分数之间的平方差。然后我们可以取这些差异平均值的平方根：

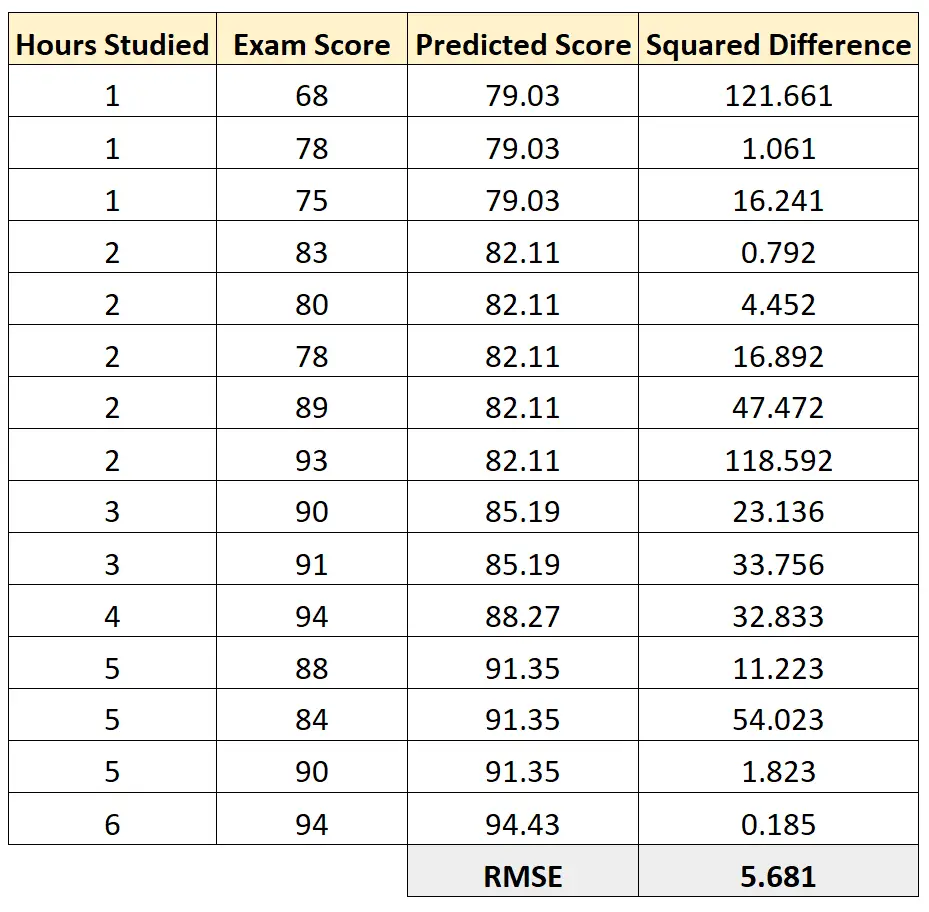
该回归模型的 RMSE 为5.681 。

回想一下，回归模型的残差是观测数据值与模型预测值之间的差异。

残差= (P _i – O _i )

金子

• P _i是数据集中^{第 i 个}观测值的预测值
• O _i是数据集中^{第 i 个}观测值的观测值

请记住，回归模型的 RMSE 计算如下：

RMSE = √ Σ(P _i – O _i ) ² / n

这意味着RMSE 表示残差方差的平方根。

这是一个值得了解的有用值，因为它让我们了解观测数据值和预测数据值之间的平均距离。

这与模型的R 平方形成对比，后者告诉我们响应变量中的方差有多少可以由模型的预测变量来解释。

不同模型的RMSE值比较

RMSE 对于比较不同回归模型的拟合度特别有用。

例如，假设我们想要建立一个回归模型来预测学生的考试成绩，并且我们想要在几个潜在模型中找到最好的模型。

假设我们拟合三个不同的回归模型并找到它们相应的 RMSE 值：

• 模型 1 的 RMSE： 14.5
• 模型 2 的 RMSE： 16.7
• 模型 3 的 RMSE： 9.8

模型 3 的 RMSE 最低，这告诉我们它能够在三个潜在模型中最好地拟合数据集。

其他资源

均方根误差计算器
如何在 Excel 中计算 RMSE
如何在 R 中计算 RMSE
如何用 Python 计算 RMSE