如何解释 roc 曲线（附示例）

逻辑回归是一种统计方法，当响应变量是二元时，我们用它来拟合回归模型。为了评估逻辑回归模型对数据集的拟合程度，我们可以查看以下两个指标：

• 敏感性：当结果实际上是积极的时，模型预测观察结果为积极的概率。
• 特异性：当结果实际上为负时，模型预测观察为负结果的概率。

可视化这两个指标的一个简单方法是创建ROC 曲线，它是显示逻辑回归模型的敏感性和特异性的图表。

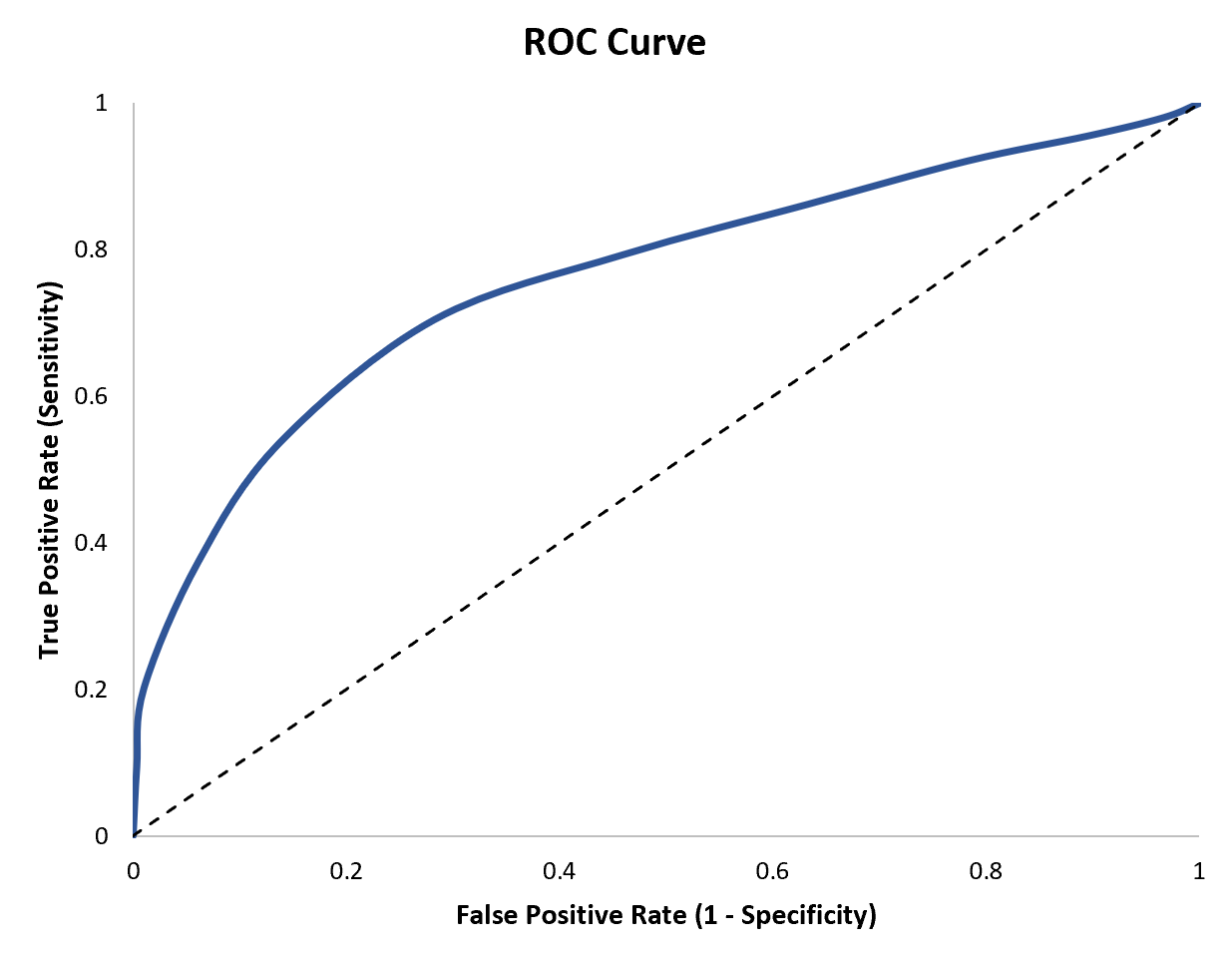
本教程介绍如何创建和解释 ROC 曲线。

如何创建 ROC 曲线

一旦我们拟合了逻辑回归模型，我们就可以使用该模型将观察结果分为两类之一。

例如，我们可以将观察结果分类为“正面”或“负面”。

真阳性率表示实际应该为阳性的观察结果的比例。

相反，假阳性率表示应该为阳性但实际上为阴性的观察结果的比例。

当我们创建 ROC 曲线时，我们为逻辑回归模型的每个可能的决策阈值绘制真阳性率与假阳性率对。

如何解释 ROC 曲线

ROC 曲线越接近图的左上角，模型就越能将数据分类。

为了量化这一点，我们可以计算AUC （曲线下面积），它告诉我们有多少图位于曲线下。

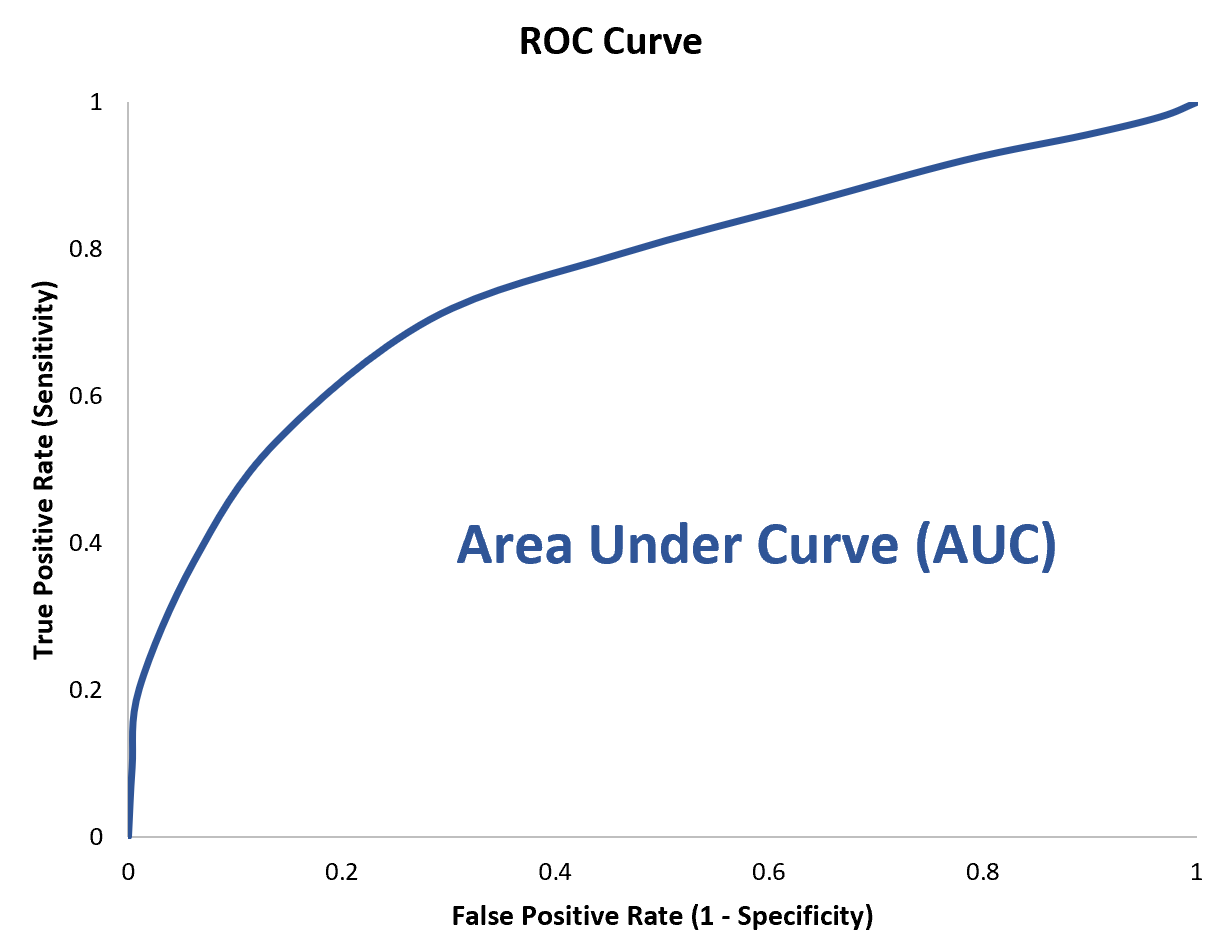
AUC 越接近 1，模型越好。

AUC 等于 0.5 的模型将是一条完美的对角线，并且代表的模型并不比进行随机分类的模型更好。

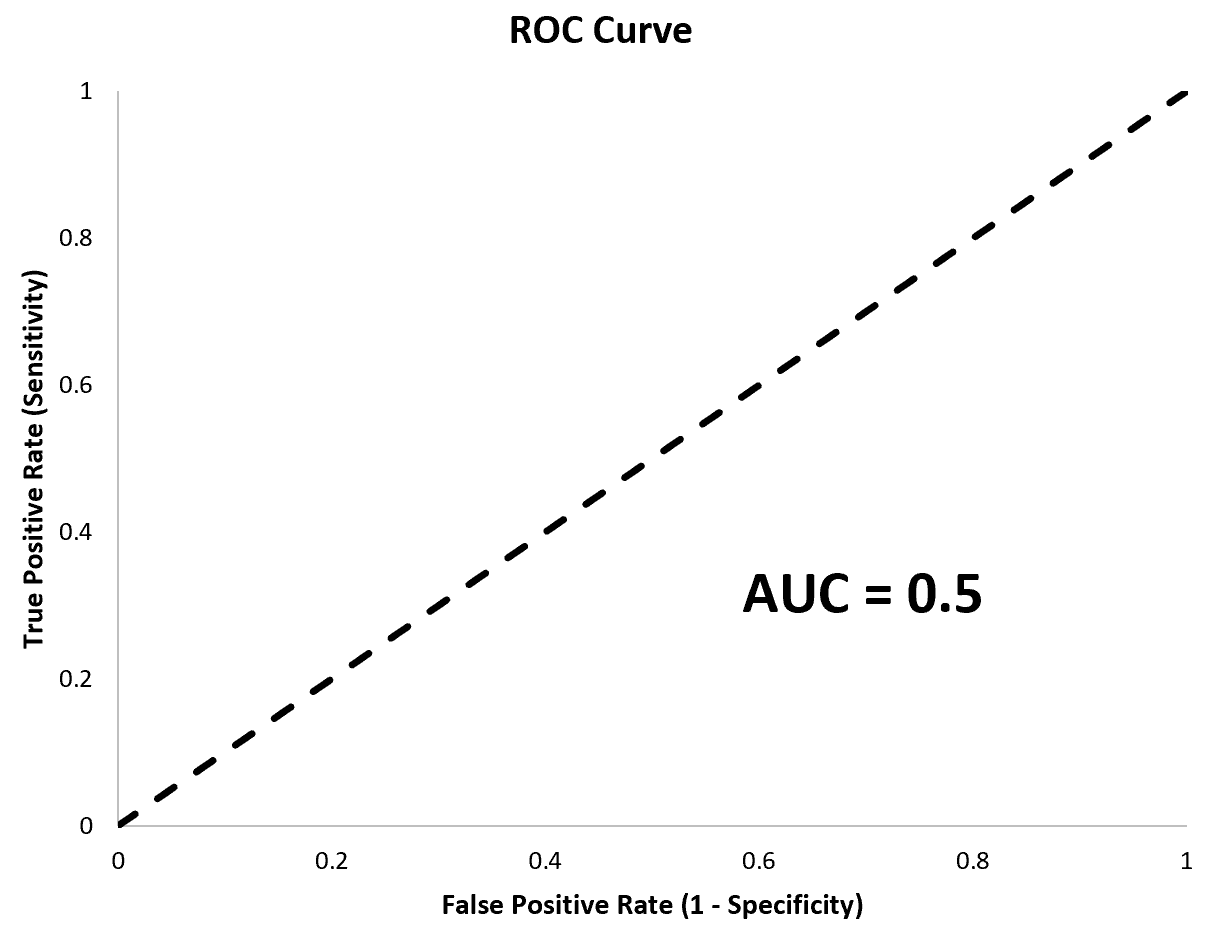
计算多个逻辑回归模型的 AUC 特别有用，因为它使我们能够了解哪个模型最适合进行预测。

例如，假设我们拟合三个不同的逻辑回归模型，并为每个模型绘制以下 ROC 曲线：

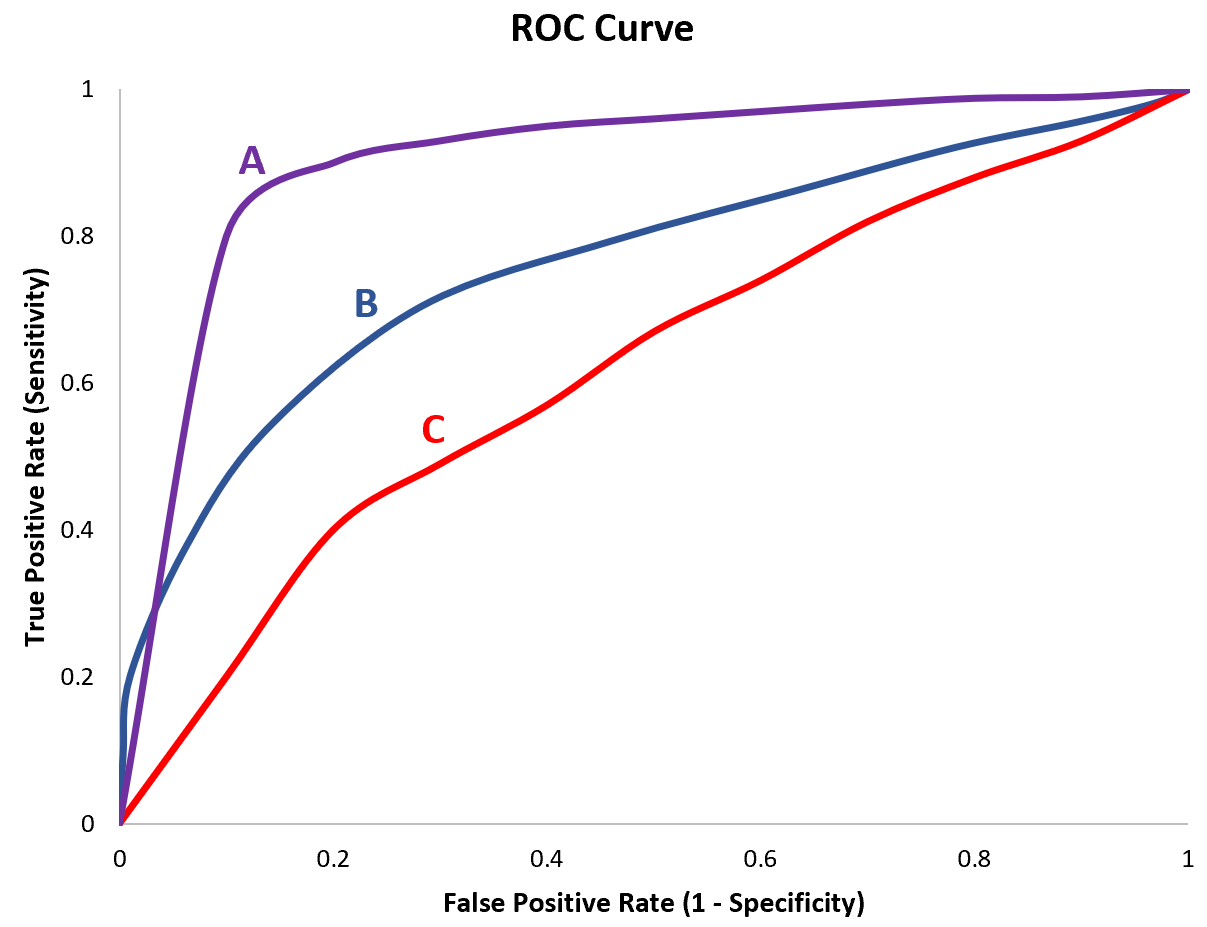
假设我们计算每个模型的 AUC 如下：

• 模型A： AUC = 0.923
• 模型 B： AUC = 0.794
• 模型 C： AUC = 0.588

模型 A 具有最高的 AUC，表明它具有最大的曲线下面积，是正确将观测结果分类的最佳模型。

其他资源

以下教程解释了如何使用不同的统计软件创建 ROC 曲线：

• 如何在 R 中绘制 ROC 曲线
• 如何在Python中绘制ROC曲线
• 如何在 Excel 中创建 ROC 曲线
• 如何在 SPSS 中创建和解释 ROC 曲线
• 如何在 Stata 中创建和解释 ROC 曲线