T-score 与 z-score:何时使用它们?
统计课程中经常让学生感到困惑的两个术语是t 分数和z 分数。
两者在执行假设检验或构建置信区间时都广泛使用,但它们略有不同。
以下是每个的公式:
得分 t = ( x – μ) / (s/√ n )
金子:
- x :样本均值
- μ :人口平均值
- s :样本标准差
- n :样本量
z 分数 = ( x – μ) / σ
金子:
- x :原始数据值
- μ :人口平均值
- σ :总体标准差
此流程图显示了您何时应该根据您的数据使用每种方法:
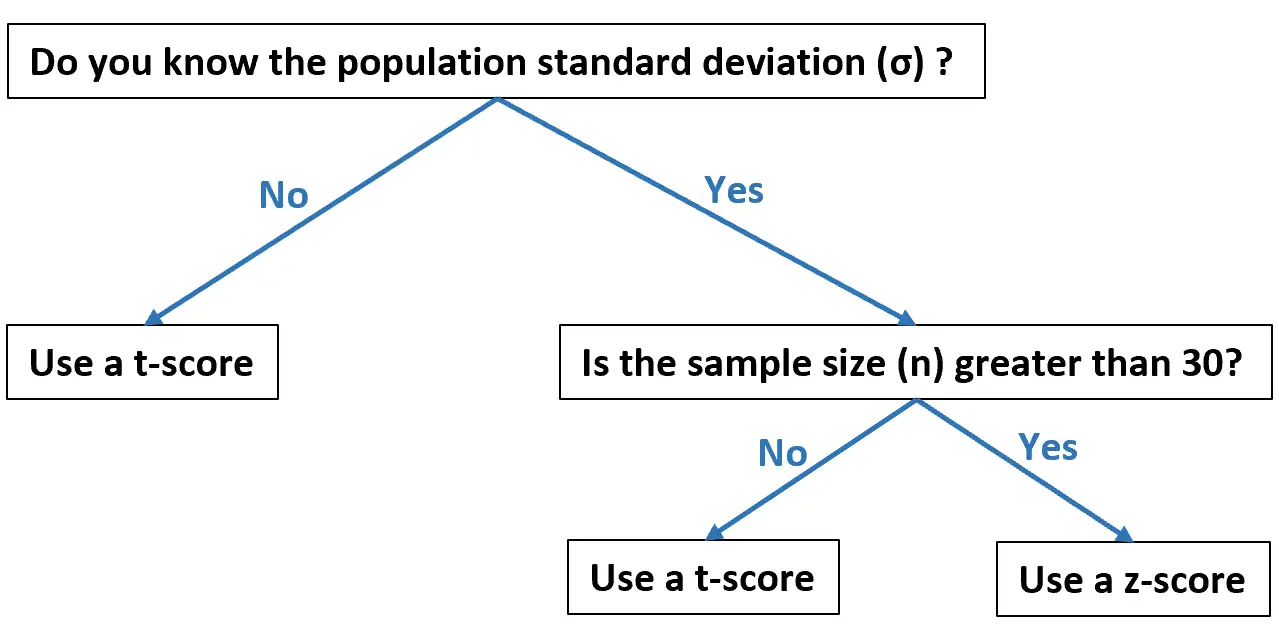
以下示例展示了如何在实践中计算 T 分数和 Z 分数。
示例 1:T 分数的计算
假设一家餐厅准备的汉堡声称平均重量为 μ = 0.25 磅。
假设我们随机抽取 n = 20 个汉堡包,发现样本平均重量为x = 0.22 磅,标准差为 s = 0.05 磅。进行假设检验以确定该餐厅生产的所有汉堡包的实际平均重量是否等于 0.25 磅。
对于此示例,我们将使用T 分数来执行假设检验,因为以下两个条件都不满足。
- 总体标准差 (σ) 已知。 (本例中未提供 σ)
- 样本量大于 30。(本例中 n=20)
因此,我们将按如下方式计算 t 分数:
- 得分 t = ( x – μ) / (s/√ n )
- t 分数 = (0.22 – 0.25) / (0.05 / √ 20 )
- t 分数 = -2.68
根据P 值 T 得分计算器,与该 t 得分对应的 p 值为0.01481 。
由于该 p 值小于 0.05,因此我们有足够的证据表明这家餐厅生产的汉堡包的平均重量不等于 0.25 磅。
示例 2:计算 Z 分数
假设一家公司生产的电池已知其使用寿命服从正态分布,平均值为 μ = 20 小时,标准差为 σ = 5 小时。
假设我们随机抽取 n = 50 节电池,发现样本平均值为x = 21 小时。进行假设检验以确定该公司制造的所有电池的真实平均寿命是否等于 20 小时。
对于此示例,我们将使用z 分数来执行假设检验,因为满足以下两个条件:
- 总体标准差 (σ) 已知。 (本例中 σ 等于 5)
- 样本量大于 30。(本例中 n=50)
因此,我们将按如下方式计算 z 分数:
- z 分数 = ( x – μ) / σ
- z 分数 = (21 – 20) / 5
- z 分数 = 0.2
根据 P 值 Z 得分计算器,与此 z 得分对应的 p 值为0.84184 。
由于该 p 值不小于 0.05,因此我们没有足够的证据表明该公司制造的所有电池的平均寿命不同于 20 小时。
其他资源
以下教程提供有关 T 分数和 Z 分数的更多信息: