如何找到点图的中心和分布
点图是一种使用堆积点显示数据集中值的频率的图。
通常,当我们创建点图时,我们想要量化中心和分布:
- Center :数据集的中心点。我们经常使用中位数来衡量这一点。
- Spread :数据集中值的分布。我们经常使用范围来衡量这一点。
通过了解这两个值,我们可以很好地了解这些值在给定数据集中的分布情况。
以下示例展示了如何在实践中查找点图的中心和范围。
示例 1:已犯错误的点图
下面的点图显示了某场比赛中篮球运动员的犯规次数:
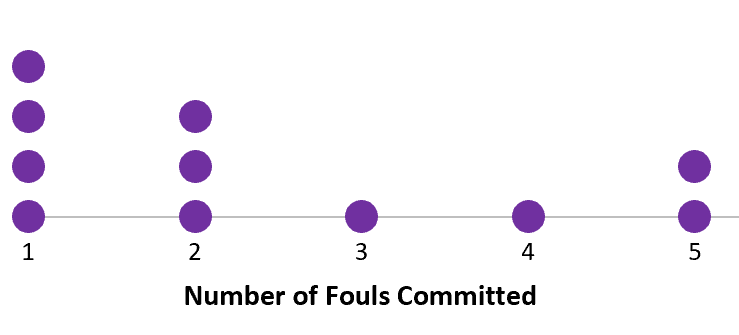
以下是如何找到这个数据集中值的中心和分布:
中心:我们可以用中位数来衡量数据集的“中心”。中位数代表数据集的中间值。为了找到这个特定数据集的中位数,我们可以列出每个值并确定中值:
数据值:1、1、1、1、2、2、2、3、4、5、5
该数据集中的中值为2 。
分布:我们可以使用范围来衡量值在数据集中的“分布”。极差表示最大值和最小值之间的差值。
在这个数据集中,我们可以看到最大值为 5,最小值为 1,因此范围可以计算为: 5 – 1 = 4 。
示例 2:测试结果的点图
下面的点图显示了特定班级学生的测试结果:
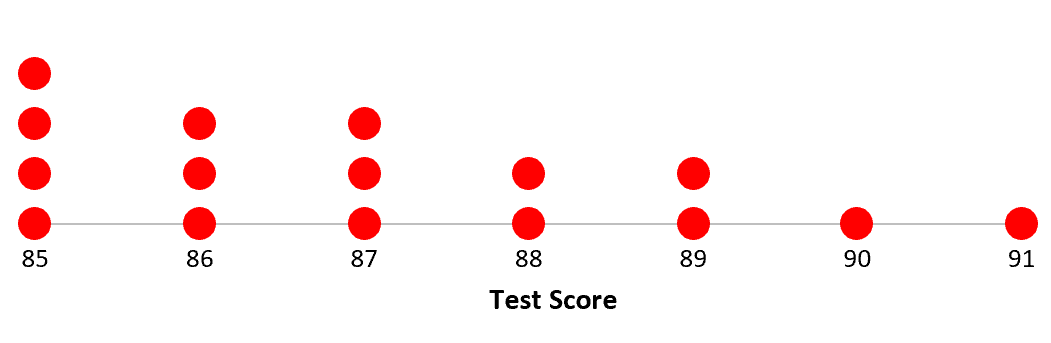
以下是如何找到这个数据集中值的中心和分布:
中心:我们可以用中位数来衡量数据集的“中心”。为了找到这个特定数据集的中位数,我们可以列出每个值并确定中值:
数据值: 85、85、85、85、86、86、86、87、87、87、88、88、89、89、90、91
该数据集有偶数个值,因此中位数将是中间两个值的平均值。中位数结果是87 。
Spread :我们可以用range来衡量数据集中数值的“散布”,它代表最大值和最小值之间的差异。
在此数据集中,我们可以看到最大值为 91,最小值为 85,因此范围可以计算为: 91 – 85 = 6 。
其他资源
以下教程解释了如何在不同的统计软件中创建点图: