帕累托分布
本文解释了统计学中的帕累托分布及其用途。您还可以看到帕累托分布图和此类概率分布的属性。
什么是帕累托分布?
帕累托分布是统计学中用于对帕累托原理建模的连续概率分布。因此,帕累托分布是一种概率分布,其中少数值的出现概率远高于其余值。
请记住,帕累托定律,也称为 80-20 规则,是一种统计原理,它指出一种现象的大部分原因是由一小部分人口造成的。
Pareto分布有两个特征参数:尺度参数x m和形状参数α。
![]()
帕累托分布最初是用来描述人口内部财富的分配的,因为大部分财富是由一小部分人口造成的。但目前帕累托分布有很多应用,例如在质量控制、经济学、科学、社会领域等。
帕累托分布以制定该分布的经济学家维尔弗雷多·帕累托 (Vilfredo Pareto) 命名。然而,他最出名的是帕累托图。
➤请参阅:什么是帕累托图?
帕累托分布表
现在我们知道了帕累托分布的定义,让我们看一下以图形方式表示的帕累托分布的几个示例。
因此,您可以在下面看到帕累托分布的密度函数图根据其特征值的样子:
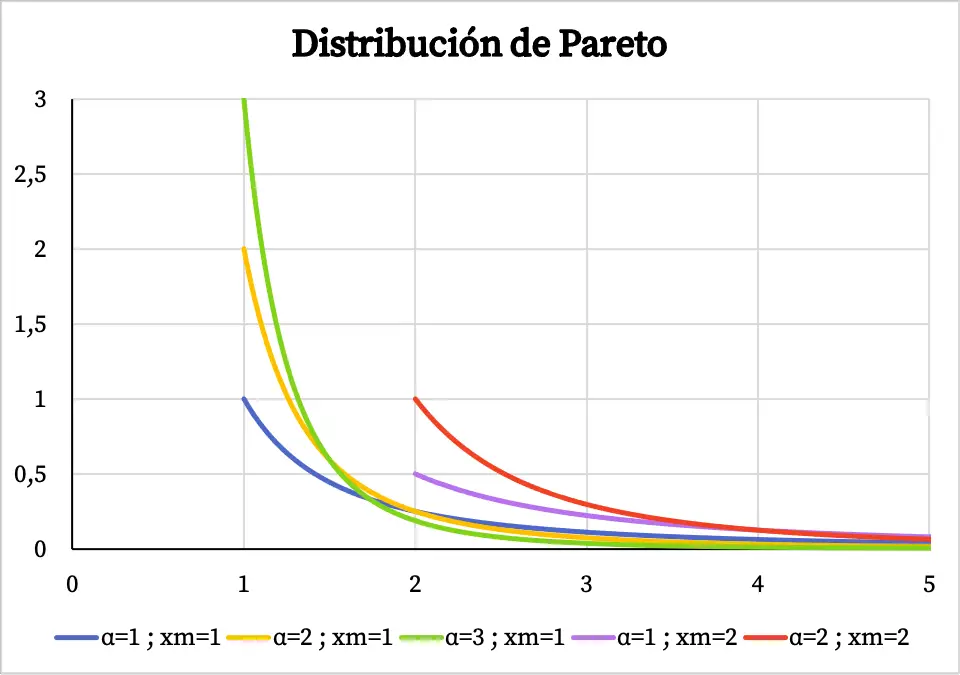
请注意,帕累托分布的域从 x m值到 +∞,这就是为什么在 x m值之前不存在密度函数的原因。
另一方面,帕累托分布的累积概率函数图如下:
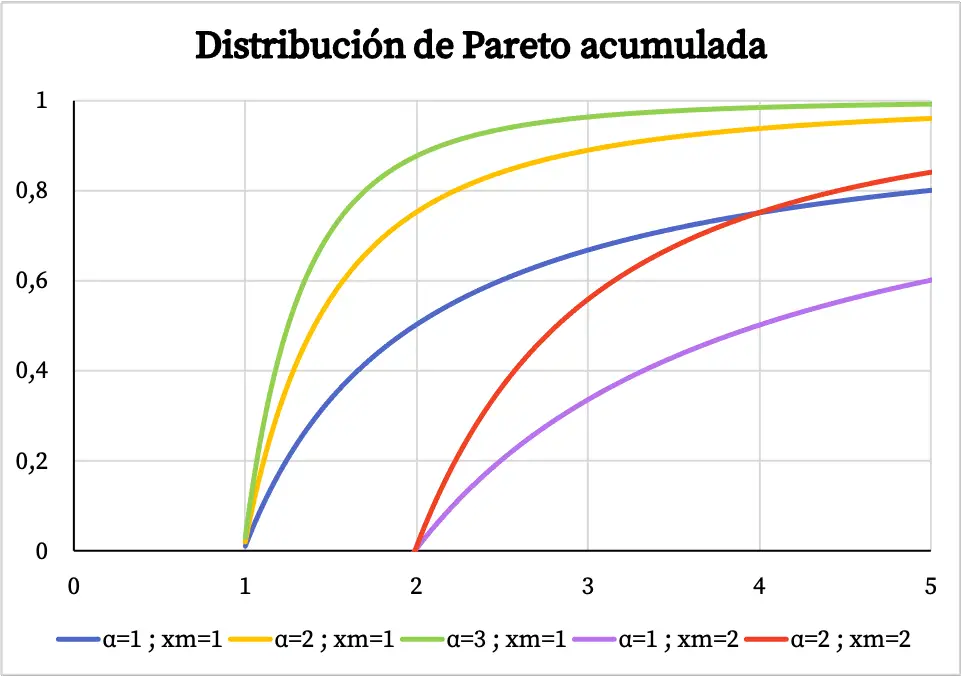
帕累托分布的特征
以下是与概率论和统计学相关的帕累托分布的最重要特征。
- 帕累托分布有两个定义其曲线的特征参数:尺度参数 x m和形状参数 α。
![]()
- 帕累托分布的域由从尺度参数到正无穷大的所有实数组成。
![]()
- 如果 α 大于 1,则帕累托分布的均值等于 α 乘以 x m与 α 减 1 的乘积。
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”></p>
</p>
<ul>
<li>帕累托分布的方差取决于分布的两个特征参数,并通过以下公式计算:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
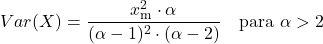
![]()
- Pareto 分布的众数相当于分布的尺度参数 x m 。
![]()
- 帕累托分布的密度函数的公式为:
![]()
- 类似地,帕累托分布的累积概率函数的公式为:
![]()
- Pareto分布的不对称系数仅取决于形状参数α,其表达式为:
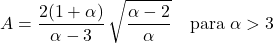
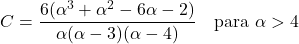
关于作者
本杰明·安德森博
大家好,我是本杰明,一位退休的统计学教授,后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识,我渴望分享我的知识,通过 Statorials 增强学生的能力。了解更多