如何在 sas 中执行双向方差分析

双向方差分析用于确定分配给两个变量（有时称为“因子”）的三个或更多独立组的平均值之间是否存在统计显着差异。

本教程提供了如何在 SAS 中执行双向方差分析的分步示例。

第 1 步：创建数据

假设植物学家想知道植物生长是否受到阳光照射和浇水频率的影响。

她种下了 30 颗种子，让它们在不同的阳光照射和浇水频率条件下生长一个月。一个月后，她记录了每株植物的高度。结果如下所示：

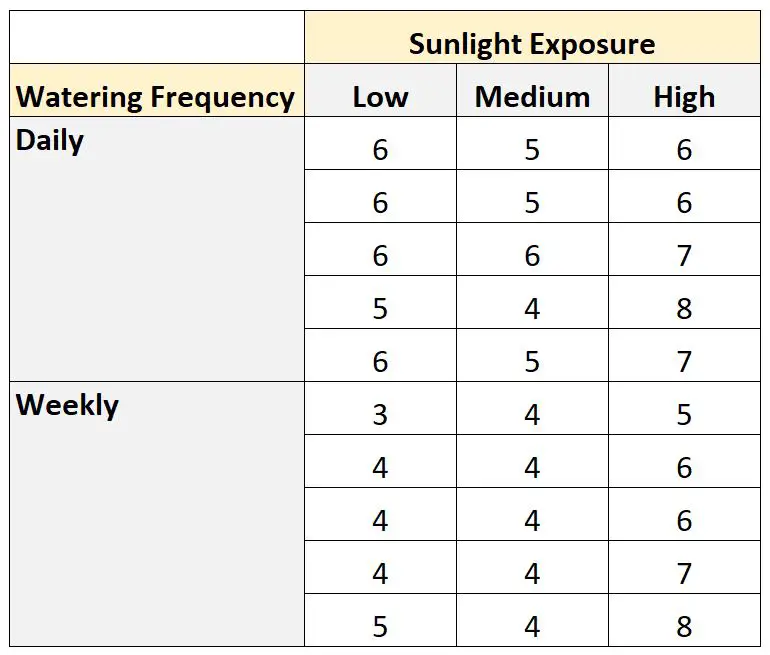
我们可以使用以下代码在 SAS 中创建此数据集：

 /*create dataset*/
data my_data;
    input water $sunlight $height;
    datalines ;
daily low 6
daily low 6
daily low 6
daily low 5
daily low 6
daily med 5
daily med 5
daily med 6
daily med 4
daily med 5
daily high 6
daily high 6
daily high 7
daily high 8
daily high 7
weekly low 3
weekly low 4
weekly low 4
weekly low 4
weekly low 5
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly high 5
weekly high 6
weekly high 6
weekly high 7
weekly high 8
;
run ;

步骤 2：执行双向方差分析

接下来，我们将使用proc ANOVA来执行双向方差分析：

 /*perform two-way ANOVA*/
proc ANOVA data =my_data;
class water sunlight;
model height = water sunlight water*sunlight;
means water sunlight / tukey cldiff ;
run ;

第 3 步：解释结果

我们要分析结果中的第一个表是 ANOVA 表：

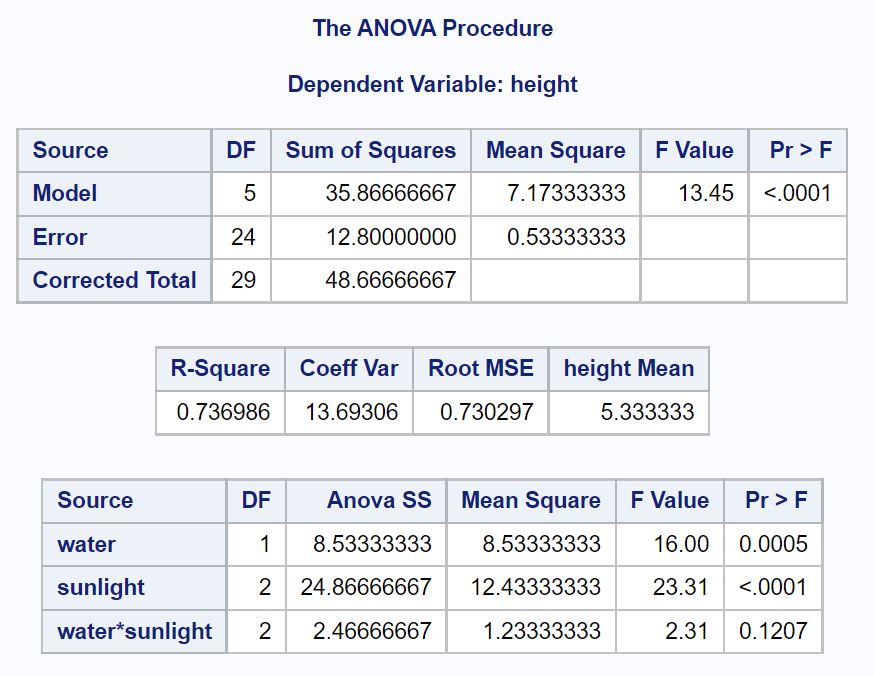
从这个表我们可以看出：

• 水的 p 值： 0.0005
• 阳光的 p 值： <.0001
• 水和阳光之间相互作用的 p 值： . 1207

这告诉我们，水和阳光是植物高度的统计显着预测因子，并且水和阳光之间不存在统计显着的相互作用效应。

接下来，我们可以检查 Tukey 事后测试的结果，以确定哪些水和阳光水平在统计上存在显着差异。

首先，我们来看看 Tukey 对水的事后比较：

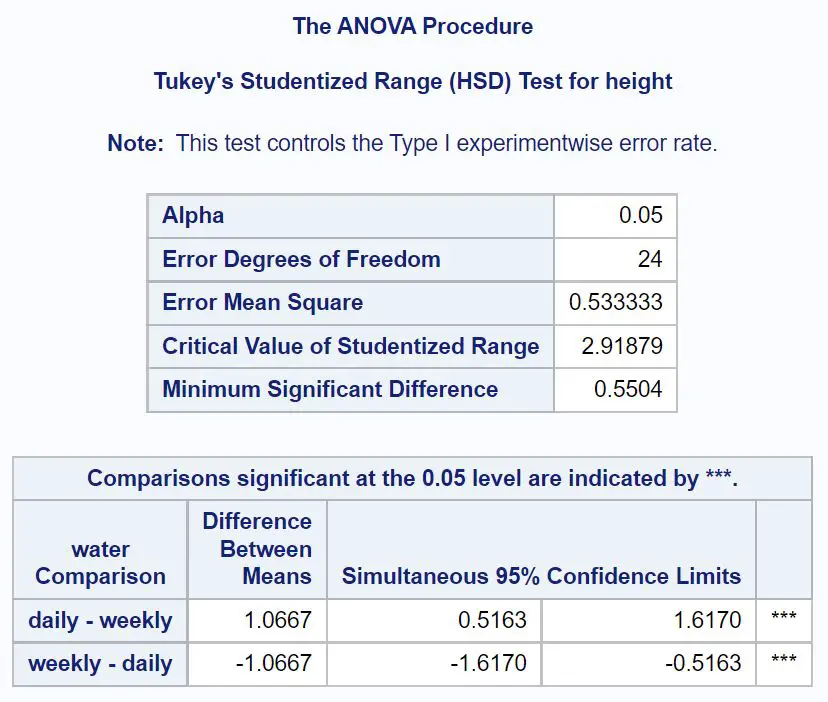
从结果中我们可以看到，每天和每周浇水的植物之间的平均高度差异为1.0667英寸。

平均大小差异的 95% 置信区间为[.5163, 1.6170] 。这意味着我们 95% 确信每天浇水的植物和每周浇水的植物之间的平均高度的真实差异在 0.5163 英寸到 1.6170 英寸之间。

首先，我们来看看 Tukey 对阳光的事后比较：

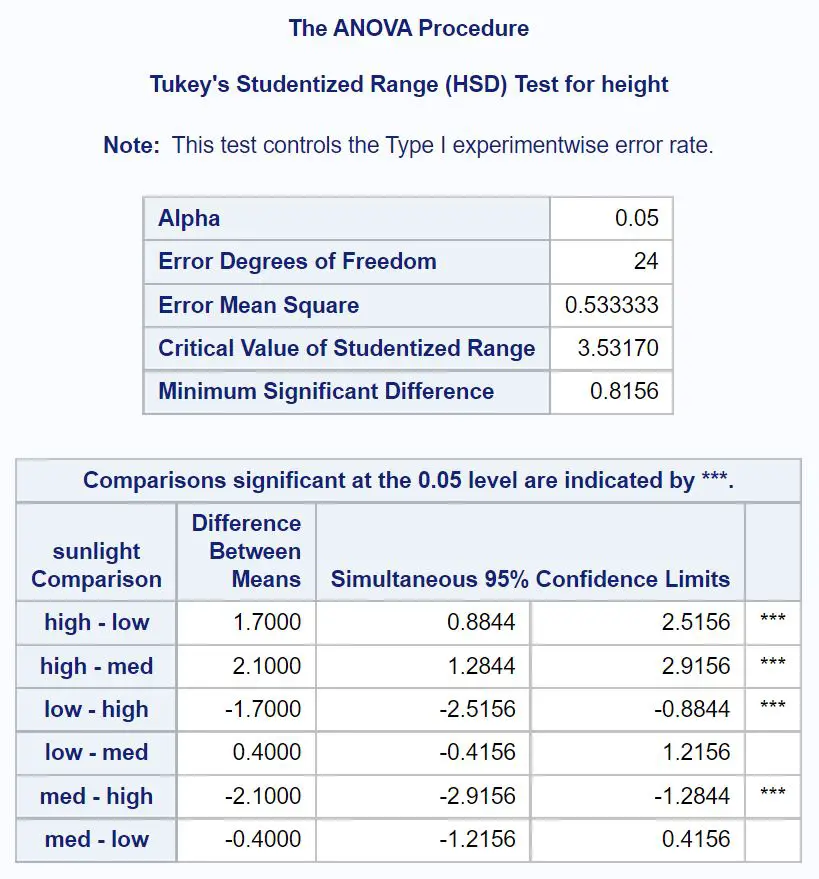
要找出哪组均值不同，我们需要查看哪些成对比较旁边有星号 ( *** )。

从表中我们可以看出，以下各组的均值在统计上有显着差异：

• 高日照或低日照 (95% CI = [.8844, 2.5156])
• 强日照或中日照 (95% CI = [1.2844, 2.9156])

第 4 步：报告结果

最后，我们可以报告双向方差分析的结果：

进行双向方差分析来分析浇水频率和阳光照射对植物生长的影响。

双向方差分析显示，浇水频率和阳光照射的影响之间不存在统计学上显着的交互作用（p = 0.1207）。

简单的手部效应分析表明，浇水频率对植物生长具有统计上显着的影响（p = 0.0005）。

简单的手效应分析表明，阳光照射对植物生长也有统计学显着影响（p < 0.0001）。

其他资源

以下教程提供有关双向方差分析的更多信息：

双向方差分析简介
单向或双向方差分析：何时使用它们？
如何手动执行双向方差分析