配对 t 检验中提出的三个假设

当一个样本中的每个观察值可以与另一个样本中的观察值相关联时，配对样本 t 检验用于比较两个样本的平均值。

此类测试对数据做出以下假设：

1. 独立性：每个观察必须独立于任何其他观察。

2. 正态性：配对之间的差异应近似呈正态分布。

3. 不存在极端异常值：差异中不应存在极端异常值。

如果不满足这些假设中的一个或多个，则配对样本 t 检验的结果可能不可靠或具有误导性。

在本教程中，我们对每个假设进行了解释，如何确定假设是否满足，以及如果违反假设该怎么办。

假设1：独立性

配对样本 t 检验假设每个观察值独立于所有其他观察值。

如何验证这个假设

验证这一假设的最简单方法是验证每个观测值是否是使用随机抽样方法收集的。

如果使用随机抽样方法（例如简单随机抽样），那么我们可以假设每个观察值独立于所有其他观察值。

如果不遵守此假设该怎么办

如果不满足这个假设，配对样本t检验的结果就完全无效。

在这种情况下，最好使用随机抽样方法收集新的观测值，以确保每个观测值都是独立的。

假设2：正态性

配对样本 t 检验假设配对之间的差异应近似呈正态分布。

这是一个至关重要的假设，因为如果对之间的差异不呈正态分布，则使用检验的 p 值得出结论是无效的。

如何验证这个假设

检验这一假设的最简单方法是简单地创建配对差异的直方图，并目视检查直方图是否具有钟形形状。

例如，如果直方图如下所示，我们会说满足正态性假设：

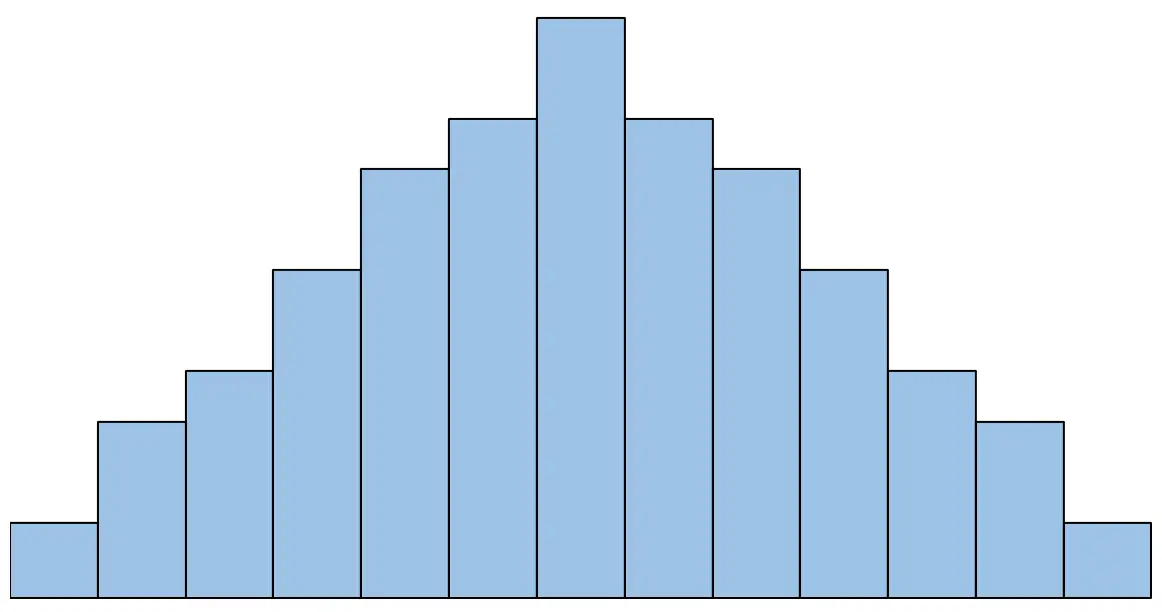
但是，如果直方图如下所示，我们会说不满足正态性假设：

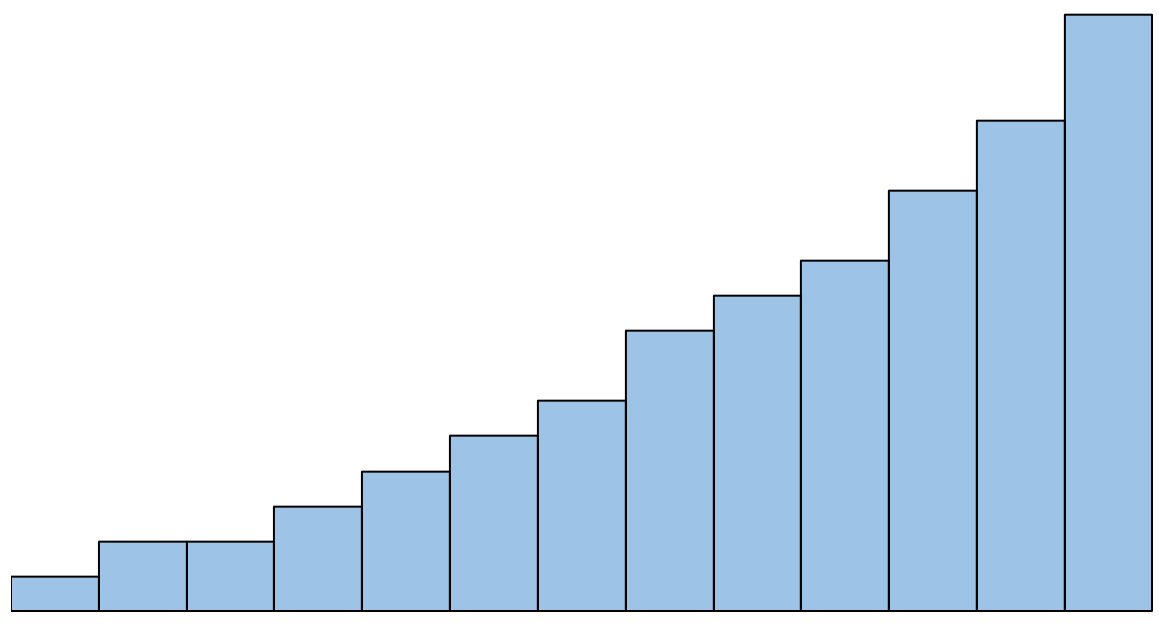
如果不遵守此假设该怎么办

如果违反了这一假设，我们可以执行Wilcoxon 符号秩检验，该检验被认为是配对样本 t 检验的非参数等效项，并且不假设配对差异呈正态分布。

假设3：不存在极端异常值

配对样本 t 检验假设数据中不存在极端异常值。

如何验证这个假设

检验这一假设的最简单方法是创建配对差异的箱线图，并目视检查是否存在任何异常值。

例如，假设配对差异的箱线图如下所示：

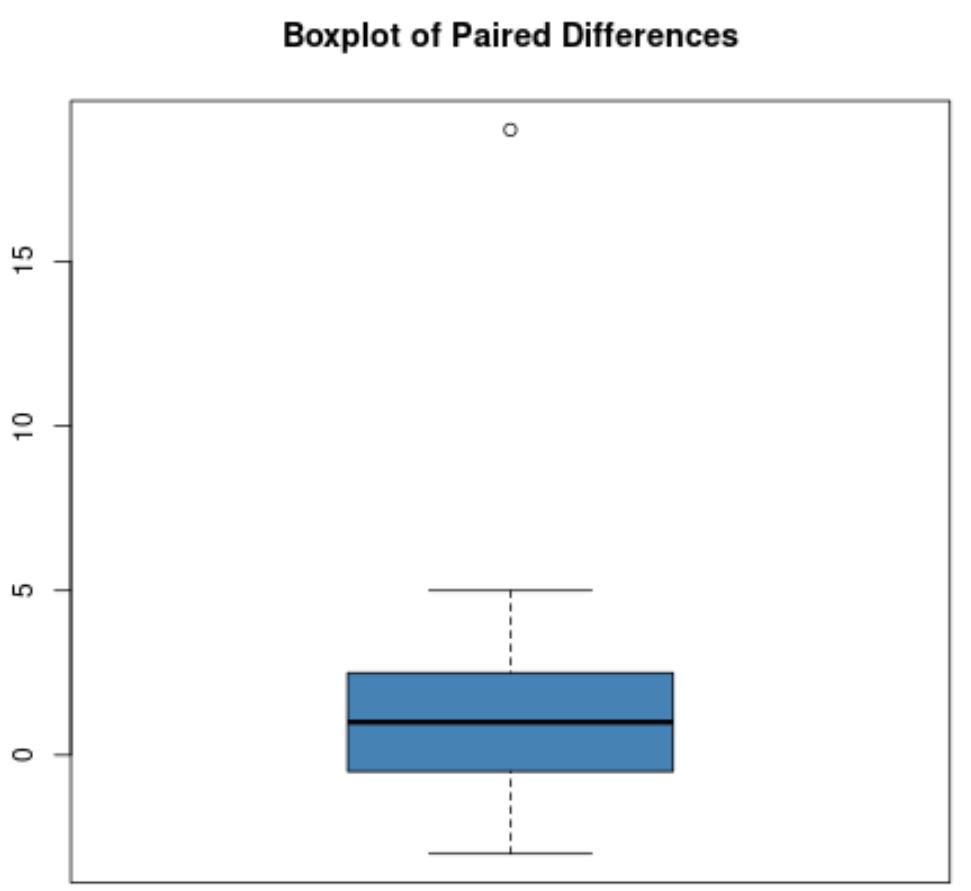
大多数配对差异接近于零，但有一个配对差异约为 19，这显然是异常值。

注意：方框图中通常使用圆圈来指示异常值。

但是，假设成对差异的箱线图如下所示：

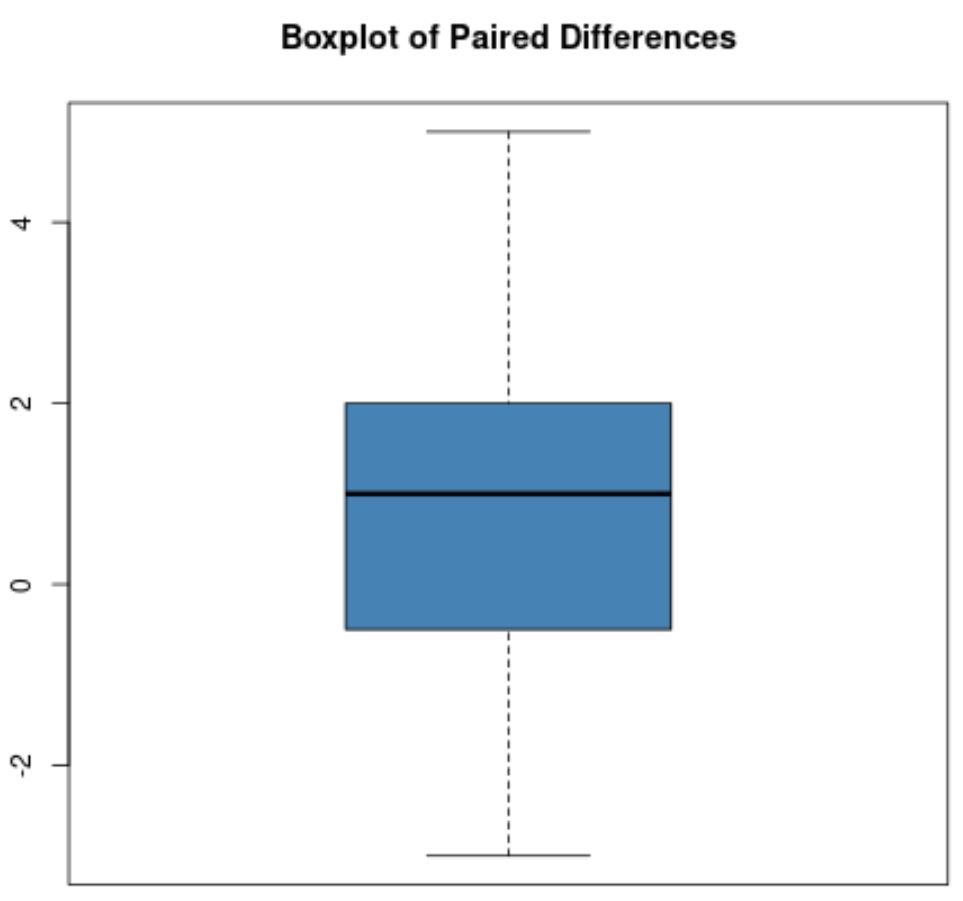
该箱线图中没有明显的异常值，因此我们假设数据中不存在极端异常值。

如果不遵守此假设该怎么办

如果违反此假设，配对样本 t 检验的结果可能会受到异常值的异常影响。

在这种情况下，如果您认为异常值代表有错误的数据点或者是数据输入错误的结果，则可以删除该异常值。

或者，您可以保留异常值，并在报告配对样本 t 检验结果时简单地记下它。

其他资源

以下教程解释了其他统计测试中所做的假设：

t 检验中提出的四个假设
卡方检验的四个假设
参数检验的四个假设