如何在 sas 中执行逻辑回归

当响应变量是二元时，逻辑回归是我们可以用来拟合回归模型的方法。

逻辑回归使用称为最大似然估计的方法来查找以下形式的方程：

log[p(X) / (1 _– p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

金子：

• X _j ：第 j^个预测变量
• β _j ：第 j^个预测变量的系数估计

方程右侧的公式预测响应变量取值 1 的对数几率。

以下分步示例展示了如何在 SAS 中拟合逻辑回归模型。

第 1 步：创建数据集

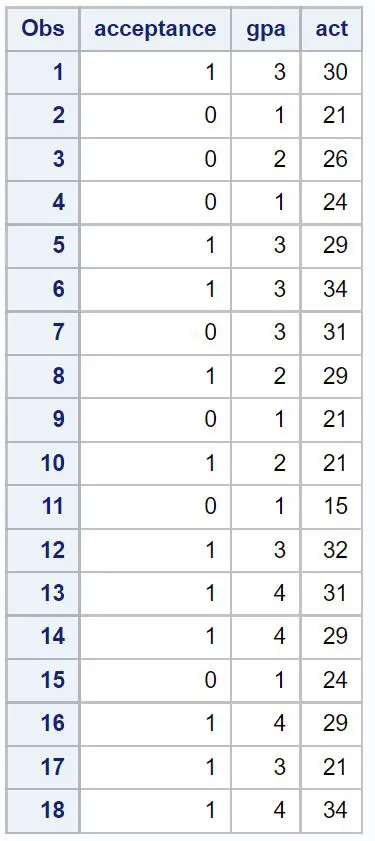
首先，我们将为 18 名学生创建一个包含以下三个变量信息的数据集：

• 被某所大学录取（1 = 是，0 = 否）
• GPA（1 至 4 等级）
• ACT 分数（1 至 36 分）

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

/*view dataset*/
proc print data =my_data;

步骤 2：拟合逻辑回归模型

接下来，我们将使用proc Logistics来拟合逻辑回归模型，使用“acceptance”作为响应变量，“gpa”和“act”作为预测变量。

注意：必须为 SAS 指定递减才能预测响应变量取值 1 的概率。默认情况下，SAS 预测响应变量取值 0 的概率。

 /*fit logistic regression model*/
proc logistic data =my_data descending ;
  model acceptance = gpa act;
run ;

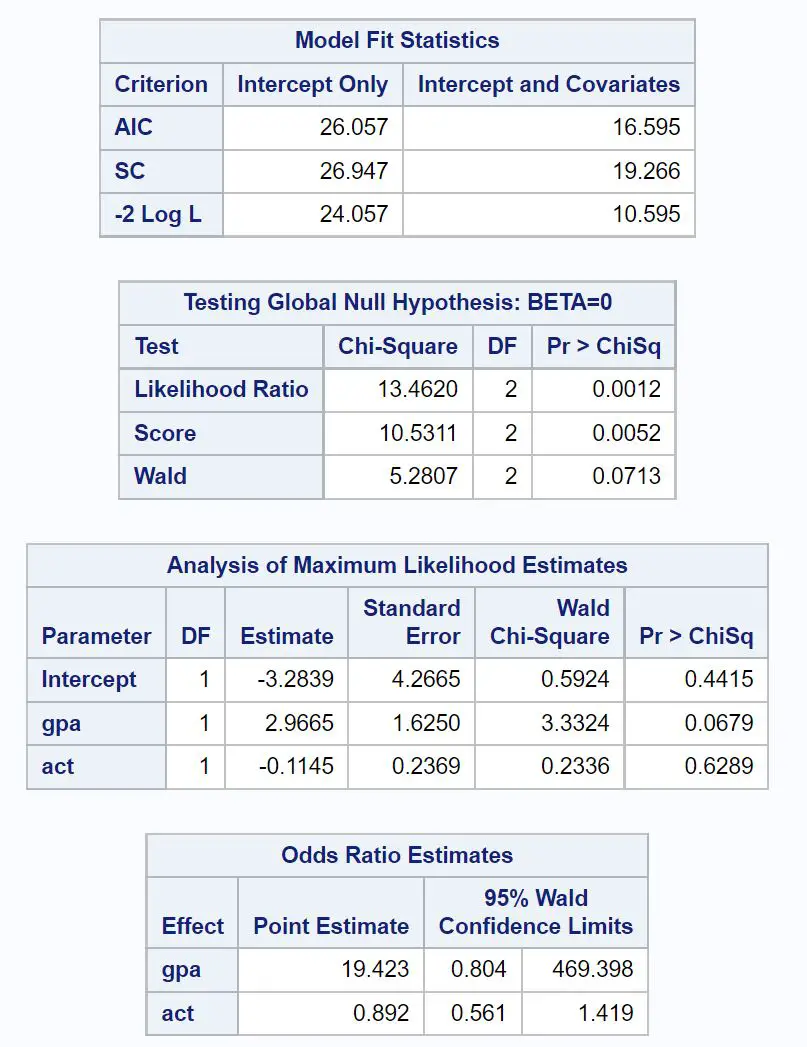
第一个感兴趣的表的标题是“模型拟合统计” 。

从该表中我们可以看到模型的 AIC 值，结果为16.595 。 AIC 值越低，模型对数据的拟合效果越好。

然而，对于什么被认为是“好的”AIC 值并没有阈值。相反，我们使用 AIC 来比较多个模型与同一数据集的拟合情况。 AIC 值最低的模型通常被认为是最好的。

下一个感兴趣的表标题为测试全局零假设：BETA=0 。

从该表中，我们可以看到似然比卡方值为13.4620 ，相应的 p 值为0.0012 。

由于该 p 值小于 0.05，这告诉我们逻辑回归模型作为一个整体具有统计显着性。

接下来，我们可以分析标题为“最大似然估计分析”的表中的系数估计。

从这个表中我们可以看到 gpa 和 act 的系数，它们表明每个变量增加一个单位，被大学录取的对数几率的平均变化。

例如：

• GPA 值每增加一个单位，被大学录取的对数几率平均增加2.9665 。
• ACT 分数每提高一个单位，被大学录取的对数几率平均下降0.1145 。

结果中相应的 p 值也让我们了解每个预测变量在预测被接受的可能性方面的有效性：

• GPA P 值： 0.0679
• ACT P 值： 0.6289

这告诉我们，GPA 似乎是大学录取的一个具有统计显着性的预测指标，而 ACT 分数似乎没有统计显着性。

其他资源

以下教程解释了如何在 SAS 中拟合其他回归模型：

如何在 SAS 中执行简单线性回归
如何在 SAS 中执行多元线性回归