如何识别 sas 中的异常值（附示例）

异常值是与数据集中的其他值异常远离的观察值。异常值可能会产生问题，因为它们会影响分析结果。

识别数据集中异常值的最常见方法是使用四分位距。

四分位距 (IQR) 是数据集中第 75 个百分位数 (Q3) 和第 25 个百分位数 (Q1) 之间的差值。它测量平均 50% 值的分布。

如果观测值是第三个四分位 (Q3) 上方四分位距的 1.5 倍或第一个四分位 (Q1) 下方四分位距的 1.5 倍，我们通常将观测值定义为异常值。

异常值 = 观测值 > Q3 + 1.5*IQR 或 < Q1 – 1.5*IQR

以下示例显示如何使用此公式来识别 SAS 数据集中的异常值。

示例：识别 SAS 中的异常值

假设我们在 SAS 中有以下数据集：

 /*create dataset*/
data original_data;
    input team $points;
    datalines ;
At 18
B24
C26
D 34
E 38
F45
G 48
H 54
I 60
Day 73
K 79
L 85
M 94
No. 98
O 221
P 223
;
run ;

/*view dataset*/
proc print data = original_data;

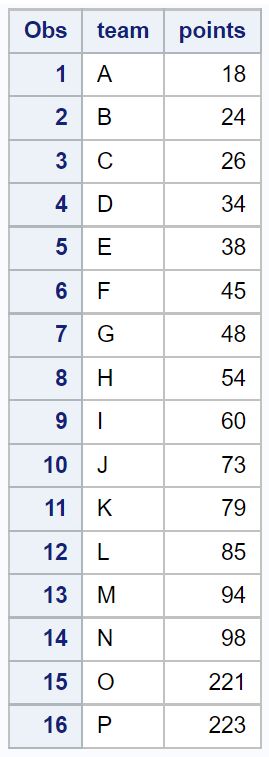
在 SAS 中识别异常值的最简单方法是创建箱线图，它会自动使用前面提到的公式来识别数据集中的异常值并将其显示为小圆圈：

 /*create boxplot to visualize distribution of points*/
ods output sgplot=boxplot_data;
proc sgplot data =original_data;
    vbox points;
run ;

/*view summary of boxplot descriptive statistics*/
proc print data =boxplot_data; 

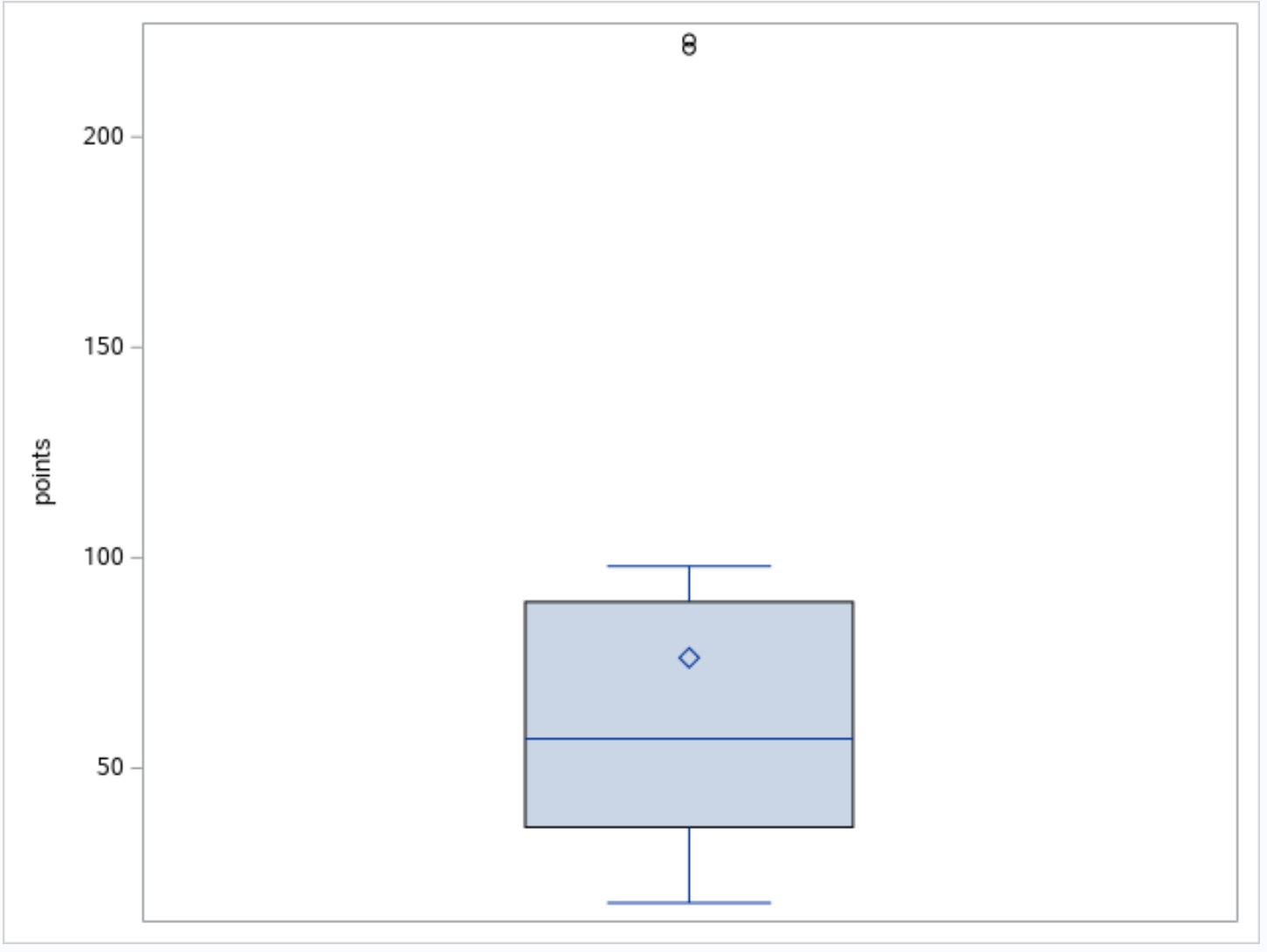
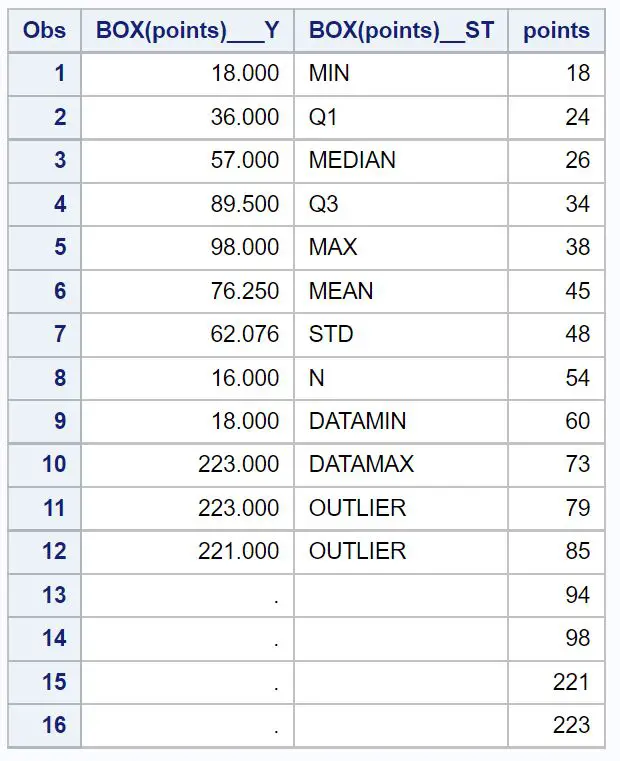
从箱线图中我们可以看到图顶部附近有两个小圆圈。这表明存在两个异常值。

在箱线图下方的表格中，我们可以看到两个异常值的精确值： 221和223 。

我们可以使用前面的公式手动检查这两个值是否为异常值：

异常值 = 观测值 > Q3 + 1.5*IQR 或 < Q1 – 1.5*IQR

四分位数范围为：Q3 – Q1 = 89.5 – 36 = 53.5。

异常值的上限为：Q3 + 1.5*IQR = 89.5 + 1.5*53.5 = 169.75。

由于221和223都大于该值，因此它们被归类为异常值。

如果需要，我们可以使用以下代码从数据集中删除这两个异常值：

 /*create new dataset with outliers removed*/
data new_data;
    set original_data;
    if points >= 221 then delete;
run ;

/*view new dataset*/
proc print data =new_data; 

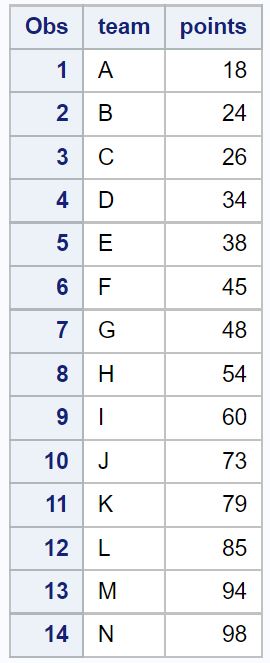
请注意，两个异常值已被删除。

其他资源

以下教程解释了如何在 SAS 中执行其他常见任务：

如何在SAS中使用过程摘要
如何在 SAS 中使用 Proc Tabulate
如何在SAS中计算相关性
如何在SAS中创建频率表
SAS中如何用零替换缺失值