下方块
本文解释了什么是统计学中的最小二乘法、什么是最小二乘法以及如何通过最小二乘准则拟合回归模型。
什么是最小二乘法?
最小二乘法是一种用于确定回归方程的统计方法。换句话说,最小二乘法是回归模型中使用的准则,用于最小化计算回归方程时获得的误差。
具体来说,最小二乘法包括最小化残差平方和,或者换句话说,它基于最小化回归模型预测值与观测值之间的差值平方和。 。 。下面我们将详细了解如何通过最小二乘准则拟合回归模型。
最小二乘法的主要特点是观测值与回归函数之间的最长距离被最小化。与其他回归标准不同,最小二乘法认为最小化大残差比最小化小残差更重要,因为大数的平方比小数的平方大得多。数字。
估计误差
为了充分理解最小二乘的概念,我们首先必须明确回归模型中的残差是什么。因此,我们将在下面看到什么是估计误差以及它是如何计算的。
在统计学中,估计误差也称为残差,是真实值与回归模型拟合值之间的差异。因此,统计残差计算如下:
![]()
金子:
-

是数据 i 的残差。
-

是数据 i 的真实价值。
-

是数据 i 的回归模型提供的值。
因此,一条数据的残差越大,回归模型对这条数据的适应能力就越差。因此,残差越小,其实际值与预测值之间的距离越小。
同样,如果一条数据的残差为正,则意味着回归模型预测的值低于真实值。如果残差为负,则表示预测值大于实际值。
最小化误差平方
现在我们知道了统计学中的残差是什么,就更容易理解如何最小化误差平方了。
误差的平方是残差的平方,因此误差的平方等于真实值与回归模型拟合的值的 2 次方之差。
![]()
金子:
-
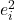
是数据 i 的残差的平方。
-

是数据 i 的真实价值。
-

是数据 i 的回归模型提供的值。
因此,最小二乘法包括通过最小化误差平方和来创建回归模型。因此,最小二乘准则基于以下表达式的最小化:
![Rendered by QuickLaTeX.com \begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0a82d4d723b77093b4d584609f372cd7_l3.png)
这就是最小二乘准则也称为最小二乘准则的原因。
正如您在前面的公式中所看到的,最小二乘准则对于最小化大残差比最小化小残差更重要。例如,如果一个残数为 3,另一个残数为 5,则它们的平方分别为 9 和 25,因此最小二乘准则将优先最小化第二个残数,然后再最小化第一个残数。
最小二乘调整
使用最小二乘准则拟合回归模型包括寻找最小化残差平方的回归模型。因此,从回归模型获得的方程将是观测值与拟合值之间的差异平方最小的方程。
请注意,在以下示例中,创建回归模型有更多标准,并且根据所选标准的不同,回归方程也不同。
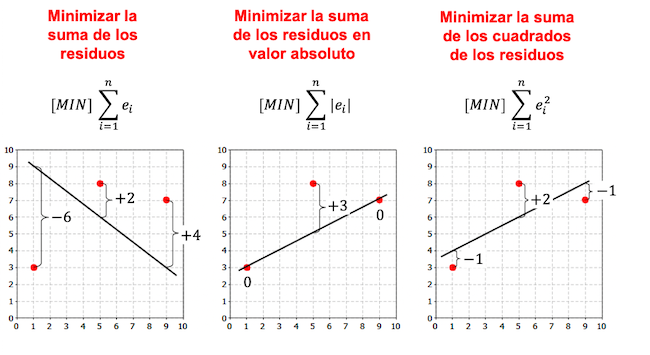
正如您在前面的示例中所看到的,从同一数据集的线性回归模型获得的线取决于所选的标准。通常,最小二乘准则用于回归模型。
在统计学中,最广泛使用的回归模型是简单线性回归模型,它使用直线来近似自变量 X 和因变量 Y 之间的关系。
![]()
因此,将数据集拟合到简单线性回归模型的公式为:

![]()
您可以通过单击以下链接查看如何使用最小二乘准则计算简单线性回归模型的示例: