贴合质量
本文解释了统计学中的拟合优度。同样,它展示了如何测量回归模型的拟合优度,此外,您将能够看到拟合优度的已解决练习。
什么是拟合优度?
在统计学中,拟合优度是指回归模型对数据样本的拟合程度。换句话说,回归模型的拟合优度是指观测集与通过回归获得的值之间的耦合程度。
因此,回归模型的拟合优度越好,它就能更好地解释所研究的数据。因此,我们希望统计模型越拟合越好。
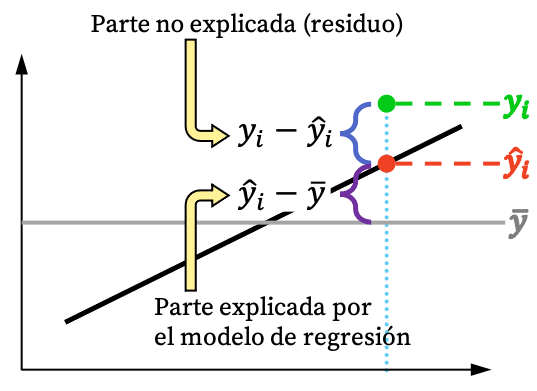
从上图中可以看出,回归模型通常无法完全解释观测值。但从逻辑上讲,回归模型可以从数据集中解释的内容越多,模型就越适合。简而言之,我们对尽可能严格的回归模型感兴趣。
回归模型的拟合优度
为了确定回归模型的拟合优度,通常使用确定系数,它是一种统计系数,表示回归模型解释的百分比。因此,模型的决定系数越高,模型就越能适应数据样本。
![]()
但需要注意的是,回归模型的变量越多,其决定系数就越高。因此,调整后的决定系数也常用于衡量模型的拟合优度。调整后的决定系数是先前系数的变体,该系数表示回归模型解释的百分比,对模型中包含的每个解释变量进行惩罚。
![]()
因此,最好使用调整后的决定系数来比较具有多个不同变量的两个模型,因为它考虑了模型中包含的变量数量。
最后需要注意的是,卡方检验也可以用来衡量回归模型的拟合优度,尽管通常使用前面两个系数的值。
良好拟合的具体例子
最后,我们将看到调整质量的解决练习,以完成对这一统计概念的吸收。
- 使用相同的数据系列,执行两种不同的线性回归模型,其结果如下表所示。最好使用哪种型号?
| 回归模型1 | 回归模型2 | |
|---|---|---|
| 决定系数 | 57% | 64% |
| 调整决定系数 | 49% | 43% |
| 解释变量的数量 | 3 | 7 |
在这种情况下,我们假设两个模型都满足之前线性回归模型的假设,因此,我们只需要分析模型的拟合优度。
回归模型2比回归模型1具有更高的决定系数,因此它似乎是一个更好的回归模型,因为它能够更好地解释数据样本。
但是,回归模型 2 的模型有 7 个自变量,而回归模型 1 只有 3 个。因此模型 2 会比第一个模型复杂得多,也更难解释。
此外,如果我们查看考虑了模型中变量数量的调整决定系数,就会发现回归模型 1 的调整决定系数高于回归模型 2。
综上所述,虽然回归模型1更好,但其调整后的决定系数高于回归模型2。回归模型2的未调整决定系数较高,这是因为它们在回归中包含了更多的变量模型 1. 模型,它增加了所述系数的值,但使模型的解释更加困难,并且肯定会使新值的预测变得更糟。
要比较具有不同数量变量的模型,最好使用调整后的决定系数,因为它会对添加到模型中的每个变量进行惩罚。正如您在这个例子中看到的,根据未调整的决定系数,回归模型2更好,但是,通过调整的决定系数我们可以知道回归模型1实际上更好。