异方差性

本文解释了统计学中的异方差是什么。此外，您还将了解导致异方差的原因、其后果是什么以及如何解决它。

什么是异方差？

在统计学中，异方差是一种呈现回归模式的特征，该回归模式意味着误差方差不是恒定的。换句话说，异方差模型意味着其误差具有不规则方差，则该模型称为异方差模型。

请记住，误差（或残差）被定义为实际值与回归模型估计值之间的差异。

构建回归模型时，使用先前的表达式计算每个观测值产生的误差。因此，当计算误差的方差在整个观察过程中不是恒定的而是变化的时，统计模型是异方差的。

虽然看起来很简单，但重要的是回归模型不呈现异方差性，因为模型的计算是基于残差的方差是恒定的这一事实，实际上它是之前的假设之一回归模型。

有某些统计检验可以检测异方差性，例如 White 检验或 Goldfeld-Quandt 检验。然而，通常通过绘制残差图，可以识别它们的异方差性。

异方差的原因

模型中异方差的最常见原因是：

• 当数据范围与平均值相比非常宽时。如果在同一个统计样本中存在很大的值和很小的值，那么得到的回归模型很可能是异方差的。
• 在回归模型中省略变量也会导致异方差。从逻辑上讲，如果模型中不包含相关变量，则其变化将包含在残差中，并且这不一定是固定的。
• 类似地，结构的变化可能会导致模型与数据集的拟合较差，因此残差的方差可能不是恒定的。
• 当某些变量的值远大于其他解释变量时，模型可能存在异方差。在这种情况下，可以将变量相对化来解决问题。

然而，某些情况本质上可能表现出异方差。例如，如果我们用一个人的食品支出来模拟一个人的收入，那么富裕的人的食品支出的变异性比穷人大得多。因为富人有时在昂贵的餐馆吃饭，有时在便宜的餐馆吃饭，不像穷人总是在便宜的餐馆吃饭。因此，回归模型很容易具有异方差性。

异方差的后果

回归模型中异方差性的后果主要如下：

• 最小二乘估计器（定义为误差平方的平均值）会损失效率。
• 最小二乘估计量的协方差矩阵的计算中会出现错误。

正确的异方差性

当得到的回归模型存在异方差时，我们可以尝试以下修正来获得异方差：

• 计算自变量的自然对数，当图中残差方差增大时，这通常很有用。
• 根据残差图，自变量的另一种变换可能更实用。例如，如果图形是抛物线形状，我们可以计算自变量的平方并将该变量添加到模型中。
• 其他变量也可以用于模型；通过删除或添加变量，可以修改残差的方差。
• 可以使用加权最小二乘准则来代替使用最小二乘准则。

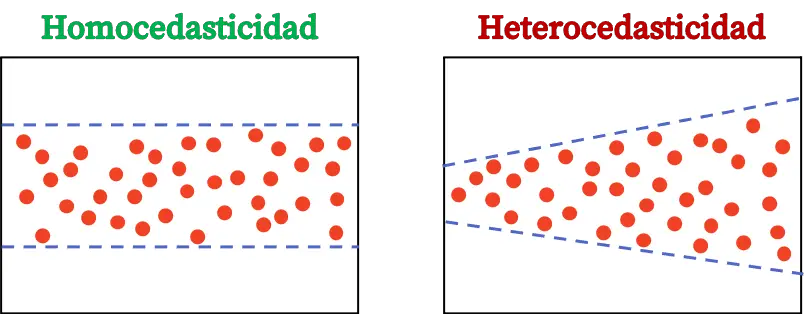
异方差和同方差

最后，我们将看到统计中的异方差和同方差有什么区别，因为这是我们必须清楚的回归模型的两个概念。

回归模型的同方差性是一种统计特征，表明误差方差是恒定的。因此，同方差模型意味着其误差的方差是恒定的。

异方差性和同方差性之间的差异在于残差方差的恒定性。如果模型残差的方差不是常数，则意味着该模型是异方差的。另一方面，如果残差的方差恒定，则意味着它是同方差的。

因此，我们需要保证我们建立的回归模型是同方差的，这样就满足残差方差恒定的假设。