三因素方差分析：定义和示例

三向方差分析用于确定三个不同因素如何影响响应变量。

三向方差分析不如单向方差分析（仅具有一个因子）或双向方差分析（仅具有两个因子）常见，但它们仍然在各种领域中使用。

每当我们进行三向方差分析时，我们都想知道每个因素和响应变量之间是否存在统计上显着的关系，以及因素之间是否存在交互作用。

本教程展示了可以使用三向方差分析的几种场景，以及如何执行该分析的示例。

何时使用三因素方差分析

以下是一些可以使用三向方差分析的场景：

场景 1：植物学

植物学家可能想要确定 (1) 阳光照射、(2) 浇水频率和 (3) 肥料类型如何影响植物生长。

在这种情况下，她可以执行三向方差分析，因为存在三个因素和一个响应变量。

场景 2：零售

零售商店的经理可能想要确定 (1) 一周中的哪一天、(2) 商店位置和 (3) 广告活动如何影响总销售额。

在这种情况下，他可以执行三向方差分析，因为存在三个因素和一个响应变量。

场景 3：医疗

医生可能想要确定 (1) 性别、(2) 饮食和 (3) 运动习惯如何影响体重。

在这种情况下，她可以执行三向方差分析，因为存在三个因素和一个响应变量。

三向方差分析：示例

假设研究人员想要确定训练计划、性别和运动项目是否会影响跳跃高度。

为了测试这一点，他可以使用以下因素进行三向方差分析：

• 1. 培训计划（计划1 vs 计划2）
• 2. 性别（男或女）
• 3. 体育组（甲组VS乙组）

唯一的响应变量是跳跃高度。

假设他收集了 40 个人的数据：

然后，他使用统计软件进行三向方差分析并得到以下结果：

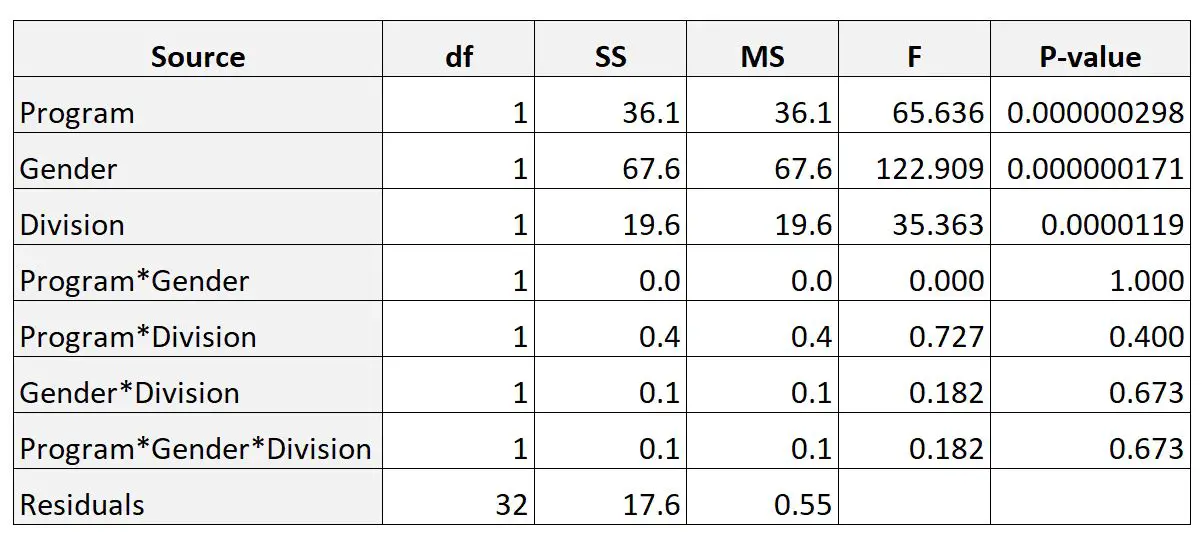
P 值列显示每个单独因素的 P 值以及因素之间的相互作用。

从结果中我们可以看出，三个因素之间的交互作用均不具有统计显着性。

我们还可以看到三个因素（项目、性别和部门）均具有统计显着性。

总之，我们可以说，训练计划、性别和级别都是提高运动员弹跳高度的重要指标。

我们还可以说，这三个因素之间不存在显着的交互作用。

注意：在实践中，我们还会计算每个项目、性别和组别的平均跳跃高度，以便我们可以确定每个因素的哪些水平与跳跃高度的增加相关。

其他资源

以下教程解释了如何在 R 和 Python 中执行三向方差分析：

如何在 R 中执行三向方差分析
如何在 Python 中执行三向方差分析