统计公式

经过 8月 1, 2023 统计数据 0 条评论

在这里您可以找到主要的统计公式。我们还为您提供了我们文章的链接，您可以在其中看到每个统计公式的应用示例，此外，您还可以使用在线计算器，从而不必进行计算并直接知道公式的结果。

集中趋势统计测度的公式

一半

要计算平均值，请将所有值相加，然后除以数据总数。因此，平均值的公式如下：

\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}

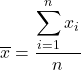
在统计学中，平均值也称为算术平均值或平均数。

➤请参阅：算术平均值计算器

中位数

中位数是所有数据从小到大排序的中间值。换句话说，中位数将有序数据集分成相等的两部分。

中位数的计算取决于数据总数是偶数还是奇数：

  • 如果数据总数为奇数，则中位数将是位于数据正中间的值。也就是说排序后的数据中位于(n+1)/2位置的值。

    • Me=x_{\frac{n+1}{2}

  • 如果数据点总数为偶数，则中位数为位于中心的两个数据点的平均值。也就是说，在有序数据的 n/2 和 n/2+1 位置处找到的值的算术平均值。

    • Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}

金子

n

为样本中数据的总数，符号Me表示中位数。

➤请参阅：中位数计算器

时尚

在统计学中，众数是数据集中出现频率最高的值，即众数是数据集中重复次数最多的值。

因此，众数没有具体的公式，但要计算统计数据集的众数，只需统计每个数据元素在样本中出现的次数，重复次数最多的数据就是众数。

众数也可以说是统计众数或众数。

➤请参阅：时尚计算器

离散度统计测量公式

标准差

标准差，也称为标准差，等于数据系列偏差平方和除以观测值总数的平方根。

因此，标准差的公式为：

\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}

➤请参阅：标准差计算器

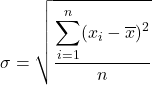
方差

方差等于观测总数的残差平方和。因此，该统计指标的公式如下：

Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}

金子：

  • X

    是要计算方差的随机变量。

  • x_i

    是数据值

    i

    。

  • n

    是观测值的总数。

  • \overline{X}

    是随机变量的平均值

    X

    。

➤请参阅：差距计算器

变异系数

在统计学中，变异系数是离散度的度量，用于确定数据集相对于其平均值的离散度。变异系数的计算方法是用数据的标准差除以平均值，然后乘以 100，以百分比形式表示该值。

CV=\cfrac{\sigma}{\overline{x}}\cdot 100

➤请参阅：变异系数计算器

整齐的

统计极差是离散度的度量，表示样本中数据的最大值和最小值之间的差异。因此，要计算总体或统计样本的范围，必须从最小值中减去最大值。

R=\text{M\'ax}-\text{M\'in}

➤参见：统计范围示例

四分位数范围

四分位距，也称为四分位距，是统计离散度的度量，表示第三个四分位数和第一个四分位数之间的差异。

因此，要计算统计数据集的四分位距，必须首先找到第三和第一四分位数，然后将它们相减。

IQR=Q_3-Q_1

中等差异

平均偏差，也称为平均绝对偏差，是绝对偏差的平均值。因此，平均偏差等于每个数据项与算术平均值的偏差之和除以数据项总数。

D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}

➤请参阅：平均偏差计算器

统计位置测量公式

四分位数

在统计学中，四分位数是将一组有序数据分为四个相等部分的三个值。因此，第一、第二和第三四分位数分别代表所有统计数据的 25%、50% 和 75%。

四分位数由大写 Q 和四分位数索引表示，因此第一个四分位数是 Q 1 ，第二个四分位数是 Q 2 ，第三个四分位数是 Q 3 。

四分位数公式为：

\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3

请注意：这个公式告诉我们四分位数的位置，而不是四分位数的值。四分位数将是位于通过公式获得的位置的数据。

然而，有时这个公式的结果会给我们一个十进制数。因此，我们必须根据结果是否为十进制数来区分两种情况：

  • 如果公式的结果是一个不带小数部分的数字，则四分位数就是上式给出的位置上的数据。
  • 如果公式结果是带小数部分的数字，则使用以下公式计算四分位值：

Q=x_i+d\cdot (x_{i+1}-x_i)

其中x i和x i+1为第一个公式得到的数所在位置的数字， d为第一个公式得到的数的小数部分。

➤请参阅：四分位数计算器

十分位数

在统计学中，十分位数是将一组有序数据分为十个相等部分的九个值。因此，第一、第二、第三……十分位数代表样本或总体的 10%、20%、30%……。

十分位数由大写字母 D 和十分位数索引表示，即第一个十分位数为 D 1 ，第二个十分位数为 D 2 ，第三个十分位数为 D 3 ，依此类推。

十分位数公式如下：

\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9

请注意：这个公式告诉我们十分位数的位置，而不是十分位数的值。十分位将是位于通过公式获得的位置的数据。

然而，有时这个公式的结果会给我们一个十进制数，因此我们必须根据结果是否是十进制数来区分两种情况：

  • 如果公式的结果是一个没有小数部分的数字，那么十分位就是位于上式所提供位置的数据。
  • 如果公式的结果是带有小数部分的数字，则使用以下公式计算十分位数值：

D=x_i+d\cdot (x_{i+1}-x_i)

其中x i和x i+1为第一个公式得到的数所在位置的数字， d为第一个公式得到的数的小数部分。

➤请参阅：十分位数计算器

百分位数

在统计学中，百分位数是将一组有序数据分为一百等份的值。因此，百分位表示数据集的百分比低于该值的值。

百分位数由大写字母 P 和百分位数索引表示，即第一个百分位数为 P 1 ，第 40 个百分位数为 P 40 ，第 79 个百分位数为 P 79等。

百分位公式为：

\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99

请注意：这个公式告诉我们百分位数的位置，但不是它的值。百分位将是位于由公式获得的位置的数据。

然而，有时这个公式的结果会给我们一个十进制数，因此我们必须根据结果是否是十进制数来区分两种情况：

  • 如果公式的结果是不带小数部分的数字，则百分位数对应于上式所提供位置的数据。
  • 如果公式结果是带小数部分的数字，则使用以下公式计算精确的百分位数：

P=x_i+d\cdot (x_{i+1}-x_i)

其中x i和x i+1为第一个公式得到的数所在位置的数字， d为第一个公式得到的数的小数部分。

➤请参阅：百分位数计算器

统计形状测量公式

不对称系数

偏度系数或偏度指数是用于确定分布偏度的统计系数。因此，通过计算不对称系数，您可以知道分布的不对称类型，而无需对其进行图形表示。

不对称系数的计算公式如下：

\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}

等效地，可以使用以下两个公式中的任意一个来计算Fisher不对称系数：

\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}

\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}

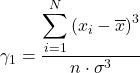
金子

E

是数学期望，

\overline{x}

算术平均值，

\sigma

标准差和

n

数据总数。

➤参见：不对称系数

峰度系数

峰度，也称为锐度，表示分布在其平均值周围的集中程度。换句话说，峰度表示分布是陡峭还是平坦。具体来说，分布的峰度越大，它就越陡（或越尖锐）。

峰度系数的计算公式如下：

\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3

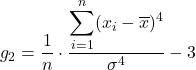
金子

x_i

是对应于观察值的值

i

,

\overline{x}

算术平均值，

\sigma

标准差和

n

数据总数。

➤请参阅：展平系数计算器

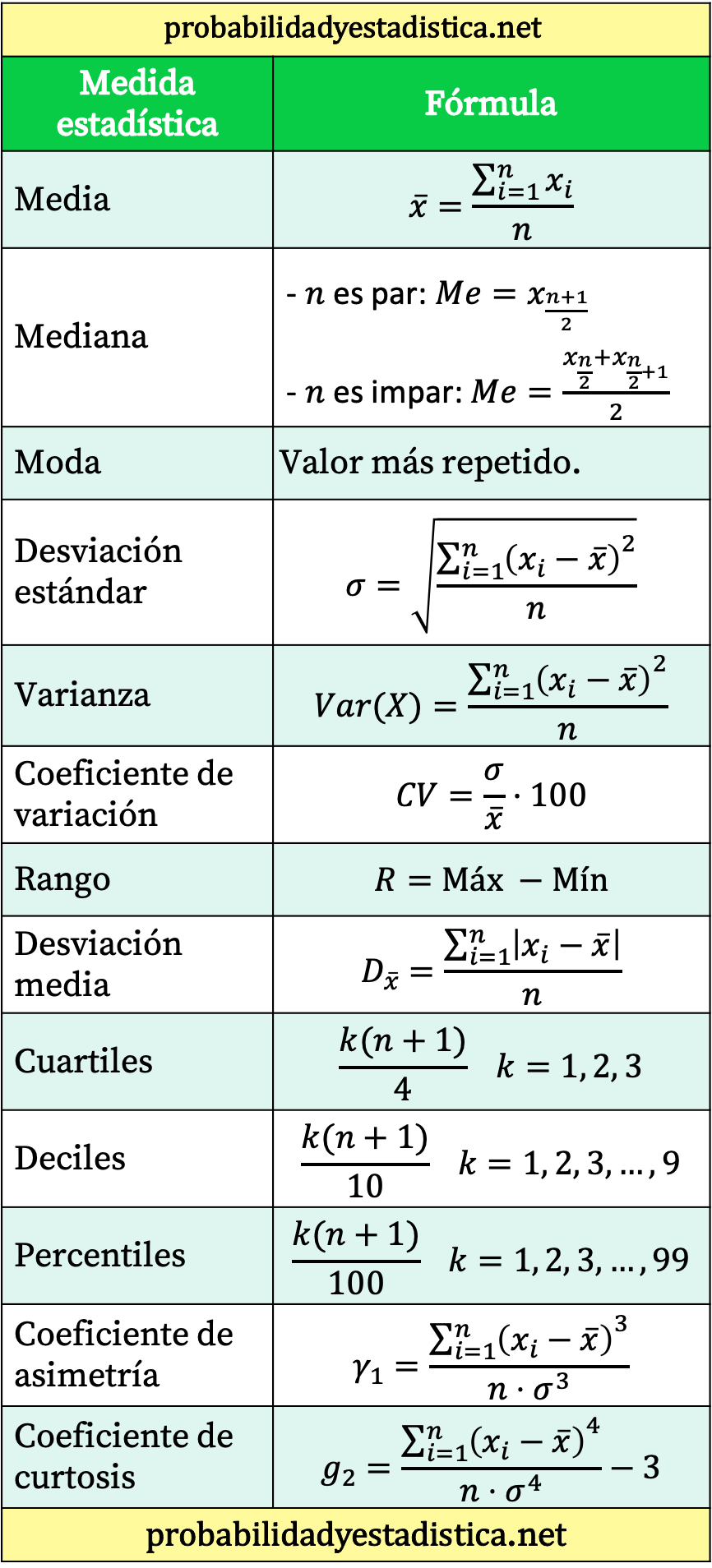
所有统计公式汇总表

最后，我们给您留下一张总结主要统计公式的表格。

统计公式
➤请参阅：概率公式

关于作者

安德森博
本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多

添加评论

您的电子邮箱地址不会被公开。 必填项已用*标注