中心极限定理
本文解释了什么是中心极限定理 (CLT) 以及它在统计学中的用途。您还将找到中心极限定理的公式是什么以及逐步解决的应用示例。
什么是中心极限定理?
在统计学中,中心极限定理,也称为中心极限定理,指出随着样本量的增加,样本均值的分布接近正态分布,而与总体的概率分布无关。
也就是说,中心极限定理说,如果我们采取足够多的样本,这些样本的平均值可以近似于正态分布。
此外,中心极限定理指出,随着样本量的增加,样本均值将接近总体均值。这使我们能够近似统计总体的参数。下面我们将看到这是如何完成的。
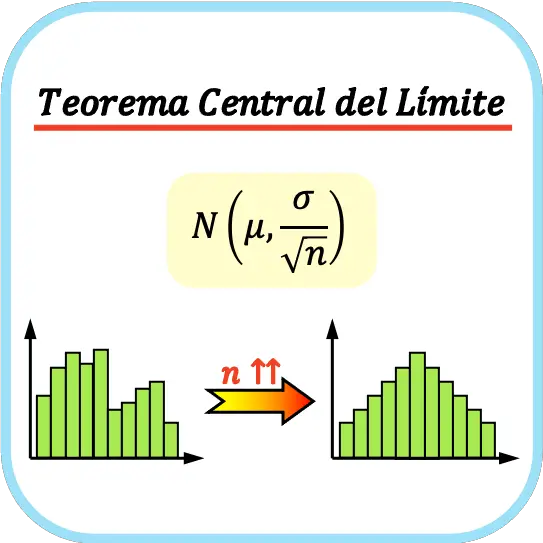
一般来说,要应用中心极限定理,样本量必须至少为 30 个观测值,尽管这取决于所研究变量的特征。
中心极限定理有很多应用,因为正态分布允许进行推断统计计算,例如假设检验或置信区间。例如,在金融领域,中心极限定理用于分析投资的回报和风险。
中心极限定理的例子
一旦我们了解了中心极限定理的定义,让我们看一个例子来充分理解它的含义。
中心极限定理的一个例子是骰子的滚动。骰子遵循离散均匀分布,因为所有结果都是等概率的。但几个结果之和的分布接近正态分布。
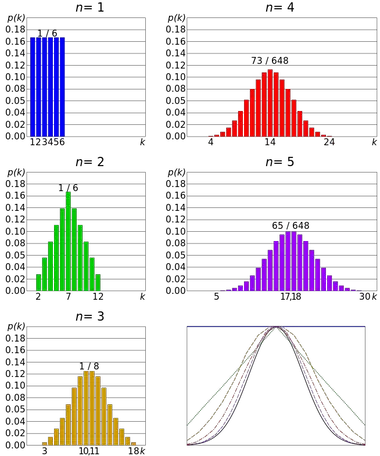
因此,抛出的次数越多,均值分布的形状就越有可能类似于正态分布图。
中心极限定理公式
中心极限定理指出,如果总体具有均值 μ 和标准差 σ,并且我们采用足够多的样本 (n≥30),则样本均值集可以近似为均值 μ 和标准差 σ 的正态分布/√n。
![]()
此外,如果X 1为由以下公式定义的正态分布:
![]()
中心极限定理的求解练习
为了让您能够完全理解这个概念,这里有一个已解决的中心极限定理练习。
- 一家公司销售用于替换某些玩具组件的零件。一枚硬币的平均重量为 300 克,标准差为 50 克。如果客户订购了一批 100 件,则该批次中件的平均重量大于 305 克的概率是多少?一批 100 件重量超过 31 公斤的概率是多少?
由于batch size很大(n=100),我们可以应用中心极限定理来解决这个问题。
因此,利用中心极限定理公式,样本均值的分布可以近似为具有以下参数的正态分布:
![]()
![]()
![]()
![]()
现在我们执行打字过程,以便我们可以找到练习要求我们拥有的概率。为此,我们需要从分布中减去平均值,然后除以标准差:
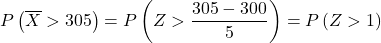 正态分布表中 Z>1 对应的值:
正态分布表中 Z>1 对应的值:
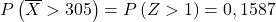
![]()
![]()
![]()
所以我们重做输入过程,然后找到问题问我们的第二个概率:
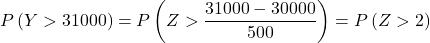
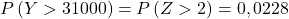 ➤参见:大数定律
➤参见:大数定律