如何在r中使用最小二乘法

最小二乘法是我们可以用来找到最适合给定数据集的回归线的方法。

要使用最小二乘法来拟合 R 中的回归线，我们可以使用lm()函数。

该函数使用以下基本语法：

 model <- lm(response ~ predictor, data=df)

以下示例展示了如何在 R 中使用此函数。

示例：R 中的最小二乘法

假设我们在 R 中有以下数据框，显示班级 15 名学生的学习小时数和相应的考试成绩：

 #create data frame
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of data frame
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

我们可以使用lm()函数使用最小二乘法来拟合该数据的回归线：

 #use method of least squares to fit regression line
model <- lm(score ~ hours, data=df)

#view regression model summary
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

根据估计结果列中的值，我们可以编写以下拟合回归线：

考试成绩 = 65.334 + 1.982（小时）

以下是如何解释模型中的每个系数：

• 截取： 对于学习 0 小时的学生，预期考试成绩为65.334 。
• 小时：每多学习一小时，预期考试成绩就会增加1,982 分。

我们可以使用这个方程来估计学生根据学习时间获得的考试成绩。

例如，如果一个学生学习了 5 个小时，我们估计他的考试成绩将为 75.244：

考试分数 = 65.334 + 1.982(5) = 75.244

最后，我们可以创建原始数据的散点图，并将拟合回归线叠加在图上：

 #create scatter plot of data
plot(df$hours, df$score, pch=16, col=' steelblue ')

#add fitted regression line to scatter plot
abline(model)

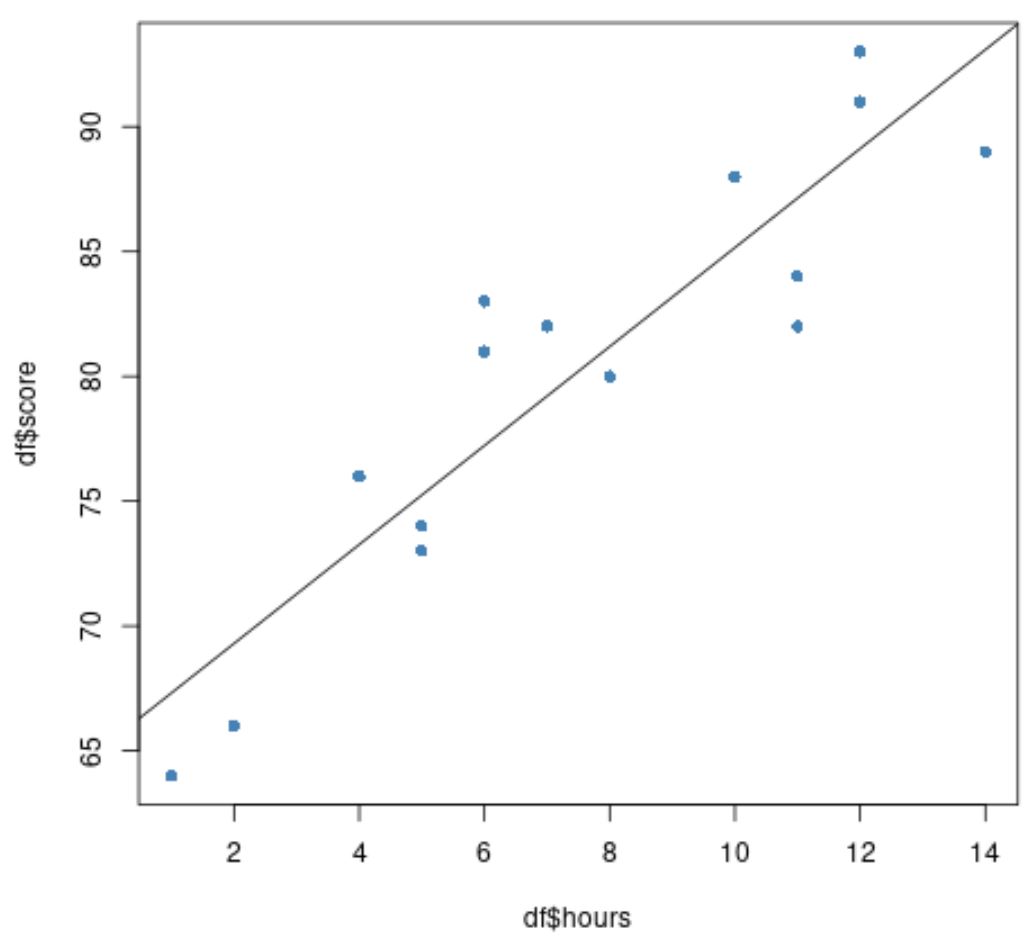
蓝色圆圈代表数据，黑线代表拟合回归线。

其他资源

以下教程解释了如何在 R 中执行其他常见任务：

如何在 R 中创建残差图
如何在 R 中测试多重共线性
如何在R中进行曲线拟合