如何确定概率分布是否有效
概率分布告诉我们随机变量取特定值的概率。
为了使概率分布有效，它必须满足两个要求：
1.每个概率必须在 0 到 1 之间。
2.概率之和必须为 1。
如果满足这两个条件，则概率分布有效。
以下示例说明如何检查不同的概率分布是否有效。
示例 1：足球比赛中进球
下面的概率分布显示了某支球队在一场比赛中进球一定数量的概率：
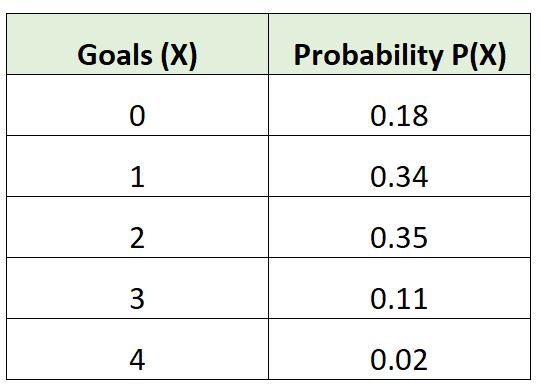
让我们检查一下这个概率分布是否满足有效的两个要求：
1. 每个概率必须在 0 到 1 之间。
我们可以看到每个个体的概率都在 0 到 1 之间。
2. 概率之和必须为 1。
我们可以看到概率之和为 1：
总和 = 0.18 + 0.34 + 0.35 + 0.11 + 0.02 = 1
这两个条件都满足，所以这个概率分布是有效的。
示例 2：一个月内的销售额
以下概率分布显示给定卖家在下个月实现一定数量销售的概率：
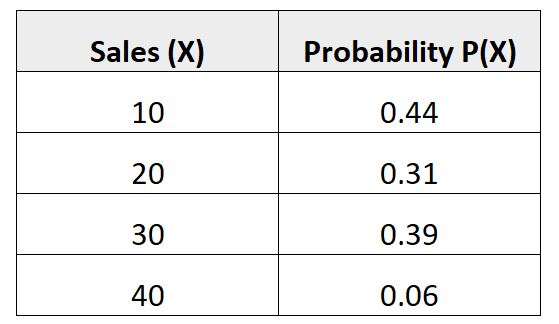
让我们检查一下这个概率分布是否满足有效的两个要求：
1. 每个概率必须在 0 到 1 之间。
我们可以看到每个个体的概率都在 0 到 1 之间。
2. 概率之和必须为 1。
我们看到概率之和不等于 1：
总和 = 0.44 + 0.31 + 0.39 + 0.06 = 1.2
这两个条件都不满足，因此该概率分布无效。
示例 3：电池故障次数
以下概率分布告诉我们特定车辆在 10 年内出现一定次数电池故障的概率：
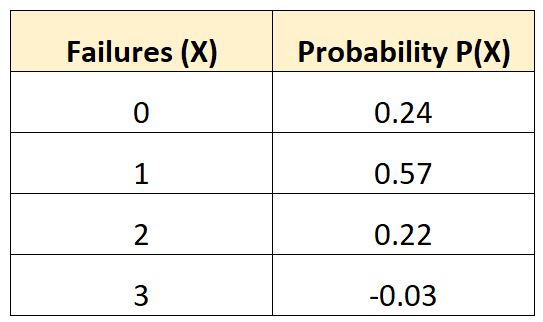
让我们检查一下这个概率分布是否满足有效的两个要求：
1. 每个概率必须在 0 到 1 之间。
我们可以看到每个个体的概率都不在0和1之间。
表中最后一个概率是负值。
2. 概率之和必须为 1。
我们可以看到概率之和为 1：
总和 = 0.24 + 0.57 + 0.22 – 0.03 = 1
这两个条件都不满足，因此该概率分布无效。
其他资源
以下教程提供有关概率分布的其他信息：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多