如何测试回归斜率的显着性
假设我们有以下数据集,显示 12 套不同房屋的面积和价格:
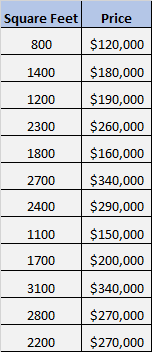
我们想知道平方英尺和价格之间是否存在显着关系。
为了了解数据的样子,我们首先创建一个散点图,其中 x 轴为平方英尺,y 轴为价格:
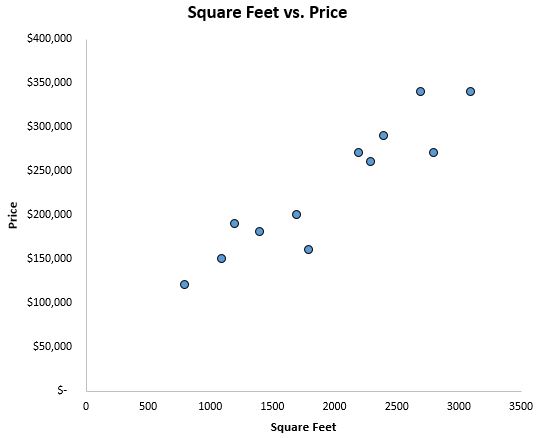
我们可以清楚地看到面积和价格之间存在正相关关系。随着面积的增加,房屋的价格也趋于上涨。
然而,为了找出平方英尺和价格之间是否存在统计上显着的关系,我们需要运行一个简单的线性回归。
因此,我们使用平方英尺作为预测变量,使用价格作为响应来运行简单的线性回归,并得到以下结果:

无论您在 Excel、SPSS、R 还是任何其他软件中运行简单线性回归,您都会得到与上图类似的结果。
请记住,简单的线性回归将产生最佳拟合线,这是最“拟合”散点图中数据的线的方程。这条最佳拟合线定义为:
ŷ = b 0 + b 1 x
其中 ŷ 是响应变量的预测值,b 0是截距,b 1是回归系数,x 是预测变量的值。
b 0的值由原点系数给出,即47588.70。
b 1的值由预测变量Square Feet的系数给出,即93.57。
所以本例中的最佳拟合线是ŷ = 47588.70+ 93.57x
以下是如何解释这条最佳拟合线:
- b 0 :当平方英尺的值为零时,预期平均价格值为 47,588.70 美元。 (在这种情况下,解释截距实际上没有意义,因为房子永远不可能有零平方英尺)
- b 1 :每增加一平方英尺,平均预期价格上涨为 93.57 美元。
因此,我们现在知道,每增加一平方英尺,平均预期价格上涨为 93.57 美元。
要了解这种增加是否具有统计显着性,我们需要对 B 1进行假设检验或构建 B 1的置信区间。
注意:假设检验和置信区间总是给出相同的结果。
构建回归斜率的置信区间
为了构建回归斜率的置信区间,我们使用以下公式:
置信区间 = b 1 +/- (t 1-∝/2, n-2 ) * (b 1的标准误差)
金子:
- b 1是回归结果中给出的斜率系数
- (t 1-∝/2, n-2 ) 是具有 n-2 自由度的 1-∝ 置信水平的临界 t 值,其中n是数据集中的观测总数
- (b 1的标准误差) 是回归结果中给出的 b 1的标准误差
对于我们的示例,以下是如何构建 B 1的 95% 置信区间:
- 回归输出的 b 1为 93.57。
- 由于我们使用 95% 置信区间,∝ = 0.05 且 n-2 = 12-2 = 10,因此根据 t 分布表,t 0.975, 10为 2.228
- ( b1的标准误差)是回归输出的 11.45
因此,B 1的 95% 置信区间为:
93.57 +/- (2.228) * (11.45) = (68.06, 119.08)
这意味着我们有 95% 的信心认为每增加平方英尺的真实平均价格涨幅在 68.06 美元至 119.08 美元之间。
请注意,0 美元不在此区间内,因此平方英尺和价格之间的关系在 95% 置信水平下具有统计显着性。
对回归斜率执行假设检验
要对回归斜率进行假设检验,我们遵循任何假设检验的五个标准步骤:
步骤 1. 陈述假设。
原假设 (H0):B 1 = 0
备择假设:(Ha):B 1 ≠ 0
步骤 2. 确定要使用的显着性水平。
由于我们在上一个示例中构建了 95% 置信区间,因此我们将在此处使用等效方法并选择使用 0.05 的显着性水平。
步骤 3. 查找检验统计量和相应的 p 值。
在这种情况下,检验统计量为t = b 1的系数 / b 1的标准误差(具有 n-2 自由度)。我们可以从回归结果中找到这些值:

因此,检验统计量t = 92.89 / 13.88 = 6.69。
使用分数为 6.69、自由度为 10 且双尾检验的T 分数到 P 值计算器,p 值 = 0.000 。
步骤 4. 拒绝或不拒绝原假设。
由于 p 值低于显着性水平 0.05,因此我们拒绝原假设。
步骤 5. 解释结果。
由于我们拒绝了零假设,因此我们有足够的证据表明,每增加平方英尺的真实平均价格涨幅不为零。