曼-惠特尼 u 检验
当样本分布不呈正态分布且样本量较小 (n < 30) 时, Mann-Whitney U 检验(有时称为 Wilcoxon 秩和检验)用于比较两个独立样本之间的差异。
它被认为是独立双样本 t 检验的非参数等效项。
以下是何时可以使用 Mann-Whitney U 检验的一些示例:
- 您想要将 A 大学的 5 名毕业生的工资与 B 大学的 5 名毕业生的工资进行比较。工资不是正态分布的。
- 您想知道两组的体重减轻是否存在差异:12 人使用饮食 A,10 人使用饮食 B。体重减轻不呈正态分布。
- 您想知道 A 班 8 名学生的分数与 B 班 7 名学生的分数是否不同。分数不服从正态分布。
在每个示例中,您想要比较两个组,抽样分布不正态,并且样本量很小。
因此,只要满足以下假设,Mann-Whitney U 检验就是合适的。
Mann-Whitney U 检验假设
在执行 Mann-Whitney U 检验之前,您必须确保满足以下四个假设:
- 普通变量或连续变量:您正在分析的变量是有序变量或连续变量。序数变量的示例包括李克特项目(例如,范围从“强烈不同意”到“强烈同意”的 5 点量表)。连续变量的示例包括身高(以英寸为单位)、体重(以磅为单位)或测试分数(从 0 到 100 进行测量)。
- 独立性:两组的所有观察结果都是相互独立的。
- 形状:两组的分布形状大致相同。
如果满足这些假设,则您可以执行 Mann-Whitney U 检验。
如何进行曼惠特尼 U 检验
为了执行 Mann-Whitney U 检验,我们遵循标准的五步假设检验程序:
1. 陈述假设。
在大多数情况下,Mann-Whitney U 检验作为双尾检验进行。原假设和备择假设写成以下形式:
H 0 :两个总体相等
H a :两个人口不相等
2. 确定用于假设的显着性水平。
确定重要性级别。常见选择为 .01、.05 和 .1。
3. 求检验统计量。
检验统计量用 U 表示,是 U 1和 U 2中较小的一个,定义如下:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
其中 n 1和 n 2分别是样本 1 和 2 的样本大小,R 1和 R 2分别是样本 1 和 2 的秩之和。
下面的示例将详细说明如何查找此检验统计量。
4. 拒绝或不拒绝原假设。
使用检验统计量,根据 Mann-Whitney U 表中的显着性水平和临界值确定是否可以拒绝原假设。
5. 解释结果。
在所提出问题的背景下解释测试结果。
执行 Mann-Whitney U 检验的示例
以下示例显示如何执行 Mann-Whitney U 检验。
实施例1
我们想知道一种新药物是否能有效预防恐慌发作。总共 12 名患者被随机分为两组,每组 6 人,并分配接受新药或安慰剂。然后患者记录他们在一个月内经历的恐慌发作的次数。
结果如下所示:
| 新药 | 安慰剂 |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
进行 Mann-Whitney U 检验,看看安慰剂组患者与新药组患者惊恐发作的次数是否存在差异。使用显着性水平 0.05。
1. 陈述假设。
H 0 :两个总体相等
H a :两个人口不相等
2. 确定用于假设的显着性水平。
该问题告诉我们应该使用 0.05 的显着性水平。
3. 求检验统计量。
回想一下,检验统计量用 U 表示,是 U 1和 U 2中较小的一个,定义如下:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
其中 n 1和 n 2分别是样本 1 和 2 的样本大小,R 1和 R 2分别是样本 1 和 2 的秩之和。
为了找到R 1和 R 2 ,我们需要结合两组的观察结果并将它们从小到大排序:
| 新药 | 安慰剂 |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
样本总数: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
排名: 1.5 , 1.5 , 3 , 4.5 , 4.5 , 6.5 , 6.5 , 8.5 , 8.5 , 10 , 11 , 12
R 1 = 样本 1 的等级总和 = 1.5+4.5+4.5+6.5+8.5+8.5 = 34
R 2 = 样本 2 的等级总和 = 1.5+3+6.5+10+11+12 = 44
接下来,我们使用样本大小 n 1和 n 2以及秩和 R 1和 R 2来找到 U 1和 U 2 。
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
我们的测试统计量是U1和U2中较小的一个,恰好是 U=13。
注意:我们还可以使用Mann-Whitney U 检验计算器来确定 U = 13。
4. 拒绝或不拒绝原假设。
使用 n 1 = 6 和 n 2 = 6,显着性水平为 0.05,Mann-Whitney U 表告诉我们临界值为 5:
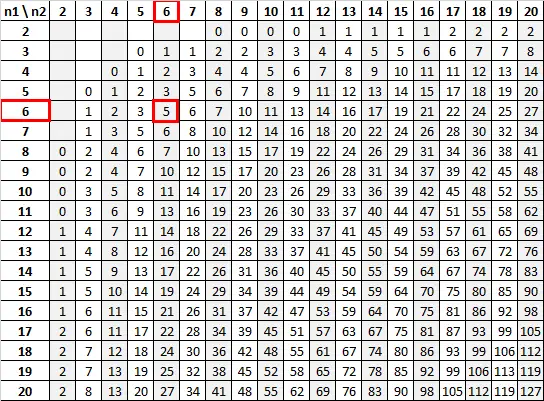
由于我们的检验统计量 (13) 大于临界值 (5),因此我们无法拒绝原假设。
5. 解释结果。
由于我们未能拒绝零假设,因此我们没有足够的证据表明安慰剂组患者经历的恐慌发作次数与新药组患者不同。
实施例2
我们想知道每周每天学习 30 分钟是否有助于学生在考试中取得更好的成绩。总共 15 名患者被随机分配到研究组或无研究组。一周后,所有学生都参加相同的考试。
两组的测试结果如下所示:
| 学习 | 没有研究 |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
执行 Mann-Whitney U 测试,看看研究组与非研究组的测试分数是否存在差异。使用显着性水平 0.01。
1. 陈述假设。
H 0 :两个总体相等
H a :两个人口不相等
2. 确定用于假设的显着性水平。
该问题告诉我们应该使用 0.01 的显着性水平。
3. 求检验统计量。
回想一下,检验统计量用 U 表示,是 U 1和 U 2中较小的一个,定义如下:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
其中 n 1和 n 2分别是样本 1 和 2 的样本大小,R 1和 R 2分别是样本 1 和 2 的秩之和。
为了找到R 1和 R 2 ,我们需要结合两组的观察结果并将它们从小到大排序:
| 学习 | 没有研究 |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
样本总数: 72、75、80、81、84、88、89、90、91、92、93、94、95、96、99 _ _ _ _ _ _ _ _ _ _ _
行: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = 样本 1 的等级总和 = 5+7+8+9+10+12+14+15 = 80
R 2 = 样本 2 的等级总和 = 1+2+3+4+6+11+13 = 40
接下来,我们使用样本大小 n 1和 n 2以及秩和 R 1和 R 2来找到 U 1和 U 2 。
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
我们的测试统计量是U1和U2中较小的一个,恰好是 U=12。
注意:我们还可以使用Mann-Whitney U 检验计算器来确定 U = 12。
4. 拒绝或不拒绝原假设。
使用 n 1 = 8 和 n 2 = 7,显着性水平为 0.01,Mann-Whitney U 表告诉我们临界值为 6:
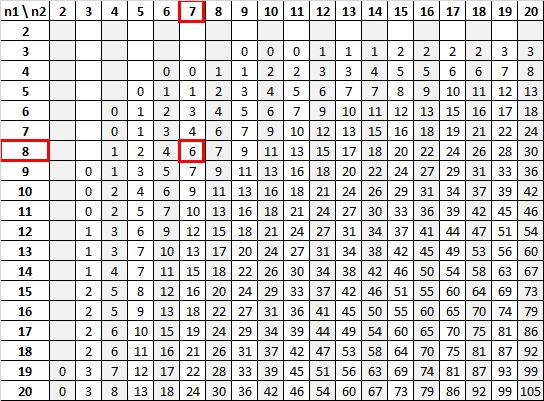
由于我们的检验统计量 (12) 大于临界值 (6),因此我们无法拒绝原假设。
5. 解释结果。
由于我们未能拒绝零假设,因此我们没有足够的证据表明学习过的学生的考试成绩与未学习过的学生不同。
其他资源
曼惠特尼 U 检验计算器
曼惠特尼 U 表
如何在 Excel 中执行曼-惠特尼 U 检验
如何在 R 中执行 Mann-Whitney U 检验
如何使用 Python 执行 Mann-Whitney U 检验
如何在 SPSS 中执行 Mann-Whitney U 检验
如何在 Stata 中执行 Mann-Whitney U 检验